Type d'échelle Y

Par défaut, l'échelle Y d'un histogramme représente l'effectif (chaque barre représente l'effectif de valeurs figurant dans la cellule spécifiée), ce qui indique l'importance de chaque cellule. Si votre public ne connaît pas assez le procédé pour comprendre les valeurs d'effectif, vous pouvez modifier le type de l'échelle Y du graphique pour convertir ces valeurs d'effectifs en pourcentages (chaque barre représente le pourcentage de toutes les valeurs figurant dans la cellule), ce format pouvant être plus représentatif aux yeux de votre public.

Par défaut, chaque barre représente l'effectif des valeurs figurant dans une cellule. Définissez le type d'échelle des Y sur Pourcentage de façon à ce que chaque barre représente le pourcentage de toutes les valeurs dans la cellule. Utilisez Densité lorsque vous souhaitez comparer des distributions et que l'effectif d'échantillon est différent. L'option Densité est également utile lorsque vous comparez les barres et que les largeurs de cellule sont inégales. La densité est obtenue par la division de la proportion d'observations par la largeur de cellule.

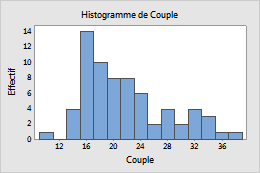
Effectif (par défaut)

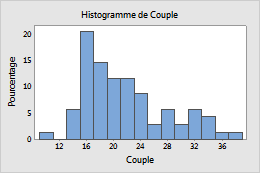
Pourcentage

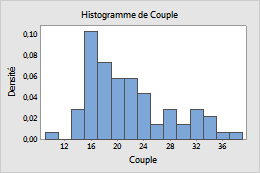
Densité

Effectif

La hauteur de chaque barre représente le nombre d'observations à l'intérieur de la cellule.

Pourcentage

La hauteur de chaque barre représente le pourcentage d'observations d'échantillons à l'intérieur de la cellule. Un histogramme doté d'une échelle de pourcentage est parfois appelé histogramme d'effectif relatif. Utilisez une échelle de pourcentage pour comparer des échantillons d'effectifs différents.

Densité

L'aire de chaque barre représente la proportion d'observations d'échantillons à l'intérieur de la cellule (proportion = aire de barre = largeur de cellule × hauteur de barre).

Accumuler les valeurs dans les cellules : (échelles d'effectif et de pourcentage uniquement) la hauteur des barres s'accumule de gauche à droite. La hauteur de chaque barre est égale à la hauteur de la cellule plus celle de toutes les cellules précédentes.

Pourcentage

Les valeurs de l'axe des Y représentent les pourcentages cumulés estimés. Le pourcentage cumulé estimé est égal à la probabilité cumulée estimée multipliée par 100.

Probabilité

Les valeurs de l'axe des Y représentent les probabilités cumulées estimées. La probabilité cumulée d'une valeur X est la probabilité qu'une observation aléatoire extraite de la population soit inférieure ou égale à X.

Minitab utilise la méthode du rang de médiane (également appelée méthode Benard) pour estimer la probabilité cumulée (r) de chaque observation :

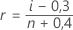
Dans cette formule, i correspond au rang de l'observation dans l'échantillon et n constitue le nombre total d'observations dans l'échantillon. Pour la plus petite valeur de l'échantillon, i = 1 et pour la plus grande valeur de l'échantillon, i = n.

Score (Diagramme de probabilité uniquement)

Les valeurs de l'axe des Y représentent des probabilités cumulées inverses.

Les valeurs de score pour la loi normale et la loi log-normale correspondent à la probabilité cumulée inverse de r, calculée à l'aide de la loi normale standard.

Les valeurs de score pour la loi exponentielle et la loi de Weibull sont calculées comme suit : LN(−LN(1−r)), LN correspondant à la fonction de logarithme népérien.

Similarité (option par défaut)

La hauteur de chaque groupe représente la similarité. La similarité s(ij) entre deux groupes i et j est calculée comme suit : s(ij) = 100 (1 - d(ij) / d(max). Si vous avez saisi la matrice D de distance d'origine pour l'analyse, d(max) est la valeur maximale en D. Si D a été calculé à partir des données, alors d(max) = 2 si vous avez sélectionné la corrélation comme mesure de distance et 1 si vous avez sélectionné la corrélation absolue comme mesure de distance.

Distance

La hauteur de chaque groupe représente la distance.