Somme
La somme est le total de toutes les valeurs des données. La somme est également utilisée dans les calculs statistiques, comme la moyenne et l'écart type.
Moyenne
Elle est calculée comme la moyenne des données, c'est-à-dire la somme de toutes les observations, divisée par le nombre d'observations.
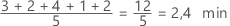
Interprétation
Utilisez la moyenne pour décrire l'échantillon avec une seule valeur qui représente le centre des données. De nombreuses analyses statistiques utilisent la moyenne en tant que mesure standard pour le centre de la loi des données.
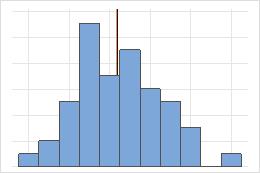
Symétrique
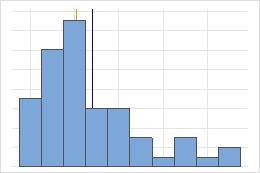
Non symétrique
Pour la loi symétrique, la moyenne (ligne bleue) et la médiane (ligne orange) sont tellement proches qu'il est difficile de distinguer les deux lignes. Toutefois, la loi non symétrique présente un asymétrie vers la droite.
EcTyp
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données sur la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit.
Etant donné que l'écart type utilise les mêmes unités que les données, il est généralement plus facile à interpréter que la variance.
Interprétation
Utilisez l'écart type pour déterminer la dispersion des données par rapport à la moyenne. Une valeur d'écart type élevée indique que les données sont dispersées. D'une manière générale, pour une loi normale, environ 68 % des valeurs se situent dans un écart type de la moyenne, 95 % des valeurs se situent dans deux écarts types et 99,7 % des valeurs se situent dans trois écarts types.
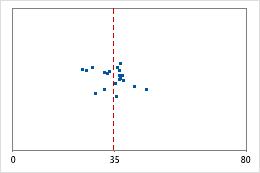
Hôpital 1
Hôpital 2
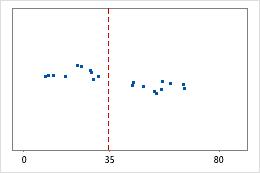
Durée jusqu'à la sortie de l'hôpital
Les administrateurs de deux hôpitaux étudient le temps que passent les patients dans le service des urgences de leurs établissements jusqu'à leur sortie. Bien que ces durées moyennes soient pratiquement identiques (35 minutes), les écarts types diffèrent de manière significative. L'écart type pour l'hôpital 1 est d'environ 6. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 6 minutes par rapport à la moyenne (ligne bleue). L'écart type pour l'hôpital 2 est d'environ 20. En moyenne, la durée qui s'écoule jusqu'à la sortie d'un patient présente un écart d'environ 20 minutes par rapport à la moyenne (ligne bleue).
Minimum
Le minimum est la valeur de données la plus petite.
Dans ces données, le minimum est de 7.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le minimum pour identifier une éventuelle valeur aberrante ou une erreur d'entrée de données. L'une des manières les plus simples d'estimer la répartition de vos données consiste à comparer le minimum et le maximum. Si la valeur minimum est très basse, même en tenant compte du centre, de la répartition et de la forme des données, recherchez la cause de cette valeur extrême.
Maximum
Le maximum est la valeur de la donnée la plus importante.
Dans ces données, le maximum est 19.
| 13 | 17 | 18 | 19 | 12 | 10 | 7 | 9 | 14 |
Interprétation
Utilisez le maximum pour identifier une éventuelle valeur aberrante ou une erreur d'entrée de données. L'une des manières les plus simples d'estimer la dispersion de vos données consiste à comparer le minimum et le maximum. Si la valeur maximale est très élevée, même en tenant compte du centre, de la répartition et de la forme des données, recherchez la cause de cette valeur extrême.
Etendue
L'étendue est la différence entre la plus grande valeur des données de l'échantillon et la plus petite. L'étendue représente l'intervalle contenant l'ensemble des valeurs des données.
Interprétation
Utilisez l'étendue pour comprendre l'importance de la dispersion des données. Une valeur d'étendue importante indique une plus grande dispersion des données. Une petite valeur d'étendue indique que les données sont moins dispersées. Comme l'étendue est calculée à l'aide de seulement deux valeurs de données, elle est plus utile avec de petits fichiers de données.
Médiane
La médiane représente le milieu de l'ensemble de données. Ce point de milieu est celui qui sépare les observations en deux moitiés égales, l'une supérieure à la valeur, l'autre inférieure. La médiane est déterminée en classant les observations, puis en prenant l'observation de rang [N + 1] / 2 dans l'ordre obtenu. Si le nombre d'observations est pair, la médiane est égale à la moyenne des observations de rang N/2 et [N/2] + 1.
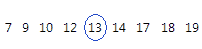
Pour les données ordonnées ci-dessous, la médiane est 13. Autrement dit, la moitié des valeurs est inférieure ou égale à 13 et l'autre moitié est supérieure ou égale à 13. Si vous ajoutez une autre observation égale à 20, la médiane est de 13,5, soit la moyenne entre la 5e observation (13) et la 6e observation (14).
Interprétation

Symétrique

Non symétrique
Pour la loi symétrique, la moyenne (ligne bleue) et la médiane (ligne orange) sont tellement proches qu'il est difficile de distinguer les deux lignes. Toutefois, la loi non symétrique présente un asymétrie vers la droite.
Somme des carrés
La somme non corrigée des carrés se calcule en mettant au carré chaque valeur de la colonne, et en calculant la somme de ces valeurs au carré. Par exemple, si la colonne contient x1, x2, ... , xn, la somme des carrés est égale à (x12 + x22 + ... + xn2). A la différence de la somme des carrés corrigée, la somme des carrés non corrigée inclut l'erreur. Les valeurs sont élevées au carré sans soustraction préalable de la moyenne.
Dénombrement total
Nombre total d'observations dans la colonne. Sert à représenter le total des valeurs présentes et manquantes.
| Dénombrement total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N
Nombre de valeurs présentes dans votre échantillon.
| Dénombrement total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
N*
Nombre de valeurs manquantes dans votre échantillon. Le nombre de valeurs manquantes correspond au nombre de cellules contenant le symbole de valeur manquante *.
| Dénombrement total | N | N* |
|---|---|---|
| 149 | 141 | 8 |
