Pour utiliser cette fonction, sélectionnez .
Calcule l'exposant auquel 10 doit être élevé pour obtenir un nombre donné. Par exemple, 102 = 100 ; par conséquent, le log en base 10 de 100 est 2. Le log en base 10 n'est défini que pour les nombres positifs. Lorsque vous multipliez un nombre par 10, vous augmentez son log de 1 ; à l'inverse, lorsque vous divisez un nombre par 10, vous diminuez son log de 1.
Syntaxe
LOGTEN(nombre)
Pour nombre, spécifiez la valeur ou la colonne des valeurs. Minitab calcule la valeur x pour laquelle 10x = nombre. Si vous entrez 0 ou un nombre négatif, Minitab stocke une valeur manquante *.
Exemple
| Expression de la calculatrice | Résultat |
|---|---|
| LOGTEN(1000) | 4 |
Utilisation
- Pour rendre davantage "normales" des données positivement asymétriques
- Pour représenter la courbure dans un modèle linéaire
- Pour stabiliser la variation à l'intérieur des groupes
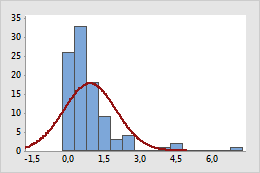
Original
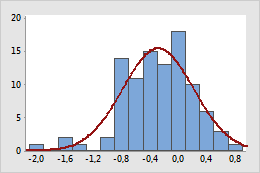
Transformation log10
Exemple de transformation des données pour les rendre davantage normales
Dans le graphique initial, les données sont positivement asymétriques, comme l'indiquent les valeurs situées tout au bout de l'extrémité droite (supérieure). La transformation log10 comprime l'extrémité supérieure et allonge l'extrémité inférieure, ce qui rend les données transformées plus normales.
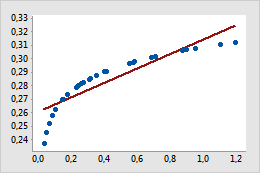
Original
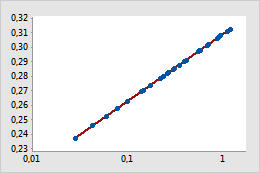
Transformation log10
Exemple de transformation des données pour rendre compte d'une courbure dans un modèle linéaire
Dans le nuage de points initial, la droite de régression simple ne modélise pas la courbure des données avec précision. Une fois l'échelle X transformée avec log10, les valeurs jalonnent la droite de régression simple.
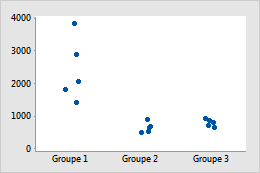
Original
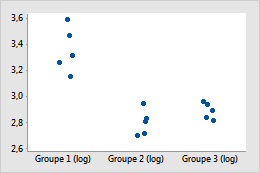
Transformation log10
Exemple de transformation des données pour stabiliser la variation à l'intérieur de groupes
Dans le diagramme des valeurs individuelles initial, le groupe 1 possède des valeurs plus élevées, si bien qu'il semble présenter une plus grande variabilité interne. Une fois les données transformées, la variation à l'intérieur des groupes semble semblable.
