Pour utiliser ces fonctions, sélectionnez .
Les fonctions Gamma, Gamma incomplet et Ln gamma sont des extensions de la fonction factorielle (1 * 2 * 3...* n), permettant de calculer les factorielles de fractions en plus des entiers positifs. La fonction Ln gamma est parfois utilisée dans les calculs à la place de la fonction gamma, car elle a moins de chance de générer des nombres très importants, susceptibles d'entraîner un dépassement de capacité.
Syntaxe
- GAMMA(forme)
- IGAMMA(limite,forme)
- LNGAMMA(forme)
Pour forme, spécifiez le nombre dont vous souhaitez prendre la fonction. Pour limite, spécifiez la limite supérieure de l'entier.
Exemples
| Expression de la calculatrice | Résultat |
|---|---|
| GAMMA(0.5) | 1,77245 |
| IGAMMA(1,2) | 0,264241 |
| LNGAMMA(3.5) | 1,20097 |
Formules
, est également appelée "fonction factorielle généralisée" et est exprimée comme suit :
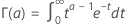
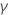, est une variation de la fonction gamma qui est définie par une intégrale avec une borne supérieure finie, et non infinie. Pour un chiffre a donné et une borne supérieure x,
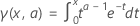
La fonction de logarithme népérien de gamma, 
, est le logarithme népérien de la fonction gamma complet.
Remarque
La fonction Gamma n'est pas définie lorsque la variable a équivaut à un entier négatif ou à zéro. La fonction Gamma incomplet n'est pas définie lorsque la variable a équivaut à un chiffre négatif ou à zéro. Minitab renvoie une valeur manquante * lorsque la fonction Gamma d'un chiffre n'est pas définie.
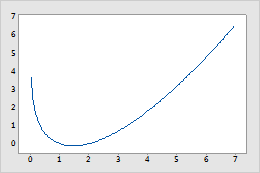
Fonction Ln gamma
Le logarithme népérien de gamma est une fonction convexe définie uniquement pour les nombres positifs.
Utilisation
La fonction gamma est essentielle dans les mathématiques pures et appliquées, les sciences et l'ingénierie, notamment dans le domaine de la thermoconduction dans les lasers et les tissus humains. En statistiques, la fonction gamma permet de calculer la fonction de densité de probabilité et la fonction de répartition de la loi gamma, qui peut être utilisée pour décrire des données asymétriques dans le sens positif.
