Select the method or formula of your choice.
In This Topic
Calculating power
One-sided power (H1: μ > μ 0)
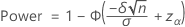
One-sided power (H1: μ < μ 0)
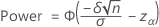
Two-sided power (H1: μ ≠ μ 0)
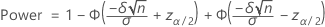
Notation
| Term | Description |
|---|---|
| μ | true value of the population mean |
| μ 0 | hypothesized value of the population mean |
| Φ | cumulative distribution function of the standard normal distribution |
| δ | difference between the true mean and the hypothesized mean |
| n | sample size |
| σ | population standard deviation |
| z α | one-sided critical value (upper α point of the standard normal distribution) |
| z α/2 | two-sided critical value (upper α/2 point of the standard normal distribution) |
| α | significance level |
Calculating sample size and difference
If you provide values for power and sample size, Minitab calculates the value of the difference. If you provide values for power and difference, Minitab calculates the value of the sample size.
Two-sided method
Minitab uses an iterative algorithm with the power equation. At each iteration, Minitab evaluates the power for a trial sample size or trial difference value, and stops when the power function equals a target power value.
One-sided method
Minitab solves directly for the value you request with the following equations:
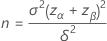
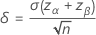
Target power and actual power
When Minitab calculates sample size, it may find that no integer value of sample size yields your target power. In such cases, Minitab displays the target value for power alongside the actual power. Actual power is a value corresponding to an integer sample size, and which is nearest to, yet greater than, the target value.
Notation
| Term | Description |
|---|---|
| n | sample size |
| σ | standard deviation |
| zα | one-sided critical value (upper α point of the standard normal distribution) |
| α | significance level |
| zβ | upper β point of the standard normal distribution |
| β | 1 – power |
| δ | difference between the population mean and the hypothesized mean |
