In This Topic
Step 1: Assess the distribution fit of the data
Minitab provides tolerance intervals for a method that uses a distribution and a nonparametric method. If you can safely assume that your data follow the distribution, then you can use the tolerance interval for the method that uses the distribution. If you cannot safely assume that your data follow the distribution, then you must try a different distribution or the tolerance interval for the nonparametric method.
To determine whether you can assume that the data follow the distribution, compare the p-value from the Anderson-Darling test to the significance level (α). A significance level of 0.05 indicates a 5% risk of concluding that the data do not follow the distribution when the data do follow the distribution.
- P-value ≤ α: The data do not follow the distribution (Reject H0)
- If the p-value is less than or equal to the significance level, you can conclude that your data do not follow the distribution. In this case, you must try a different distribution or the tolerance interval for the nonparametric method.
- P-value > α: You do not have enough evidence to conclude that the data do not follow the distribution (Fail to reject H0)
- If the p-value is larger than the significance level, you do not have enough evidence to conclude that the data do not follow the distribution. In this case, you can use the tolerance interval for the method that uses the distribution.
Key Results: Probability plot and p-value
The probability plot shows that the plotted points fall along the Weibull distribution fitted line, which indicates that the data follow a Weibull distribution. Also, the p-value of the goodness-of-fit test is 0.178, which is greater than the significance level of 0.05. Because you cannot conclude that the data do not follow the Weibull distribution, you can use the interval for the Weibull distribution.
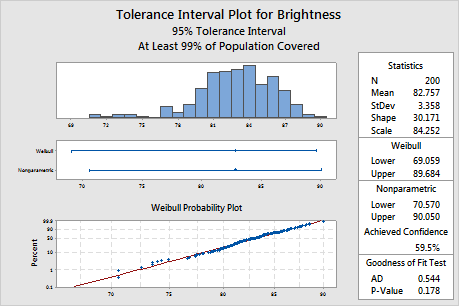
Step 2: Examine the tolerance interval from the appropriate method
- Two-sided
- Use a two-sided interval to determine an interval that contains a certain minimum percentage of the population measurements.
- Upper bound
- Use an upper bound to determine a limit that exceeds a certain minimum percentage of population measurements.
- Lower bound
- Use a lower bound to determine a limit that is less than a certain minimum percentage of population measurements.
