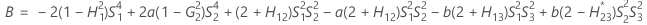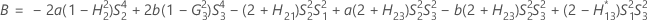In This Topic
- Confidence interval for the ratio of the repeatability variance and the total variance
- Confidence interval for the ratio of the reproducibility variance and the total variance
- Confidence interval for the ratio of the part variance and the total variance
- Confidence interval for the ratio of the gage variance and the total variance
Confidence interval for the ratio of the repeatability variance and the total variance
There are two possible calculation methods. Minitab first calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses the Satterthwaite approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
MLS method


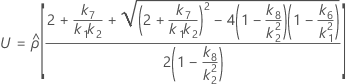
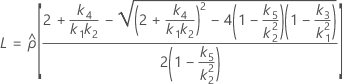
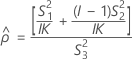
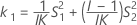
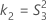
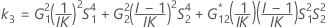
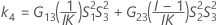

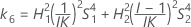
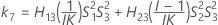

The two conditions for the existence of the lower and the upper bounds using the MLS method are:
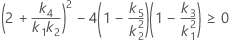
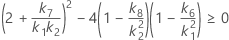
If the two conditions are not satisfied, Minitab cannot use this method to construct the lower and upper bounds. Minitab will use the Satterthwaite approximation to calculate the lower and upper bounds.
Satterthwaite approximation
The formulas for the lower and upper bounds still hold except L and U are defined as follows:
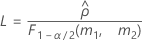
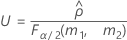
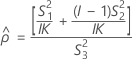
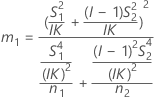
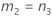
Notation
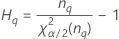
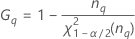
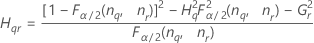
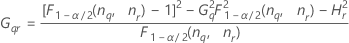
| Term | Description |
|---|---|
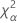 | the α * 100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Confidence interval for the ratio of the reproducibility variance and the total variance
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. To calculate the one-sided confidence bounds, replace α/2 with α in H and G.
MLS method
The lower and upper bounds for an approximate (1–α) * 100% confidence interval are calculated by solving quadratic equations.
- Lower bound
-

- Upper bound
-

Second method
If B2– 4AC < 0, there is no solution to the quadratic equation. In this case, Minitab uses the second method to estimate the confidence intervals. The lower and upper bounds for an approximate (1–α) * 100% confidence interval are calculated as follows:
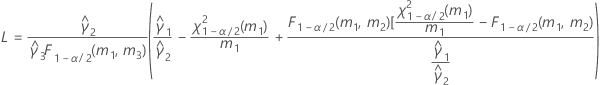
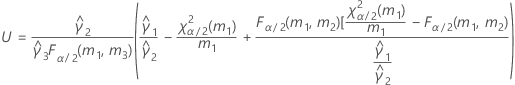
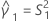
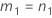
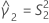
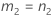

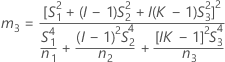
Notation
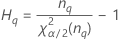
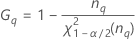
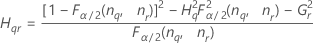
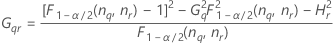
| Term | Description |
|---|---|
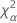 | the α * 100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Confidence interval for the ratio of the part variance and the total variance
There are two possible calculation methods. First, Minitab calculates the bounds using the modified large-sample (MLS) method. If certain conditions are not met during the calculations, then Minitab uses an alternate approximation. Replace α/2 with α in H and G to calculate the one-sided confidence bounds.
MLS method
- Lower bound
-

- Upper bound
-

Second method
If B2– 4AC < 0, there is no solution to the quadratic equation. In this case, Minitab uses the second method to estimate the confidence intervals. The lower and upper bounds for an approximate (1–α) * 100% confidence interval are calculated as follows:
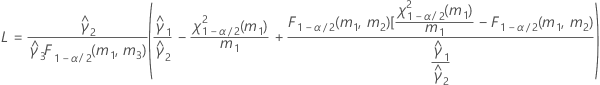
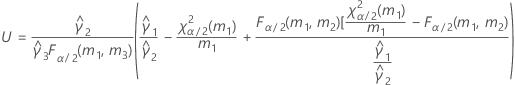

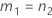

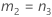

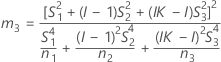
Notation
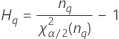
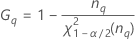
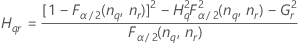
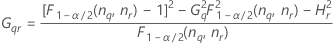
| Term | Description |
|---|---|
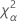 | the α * 100 percentile of the chi-square distribution with nq degrees of freedom |
| J | the number of operators |
| I | the number of parts |
| K | the number of replicates |
Confidence interval for the ratio of the gage variance and the total variance
Lower bound = 1 – (lower bound of the CI for the ratio of the part variance and the total variance)
Upper bound = 1 – (upper bound of the CI for the ratio of the part variance and the total variance)