
Support
Got questions? Find the help you need, whenever you need it.

Featured Support Videos
Watch helpful videos to learn how to get started using our software, uncover product features, and more.
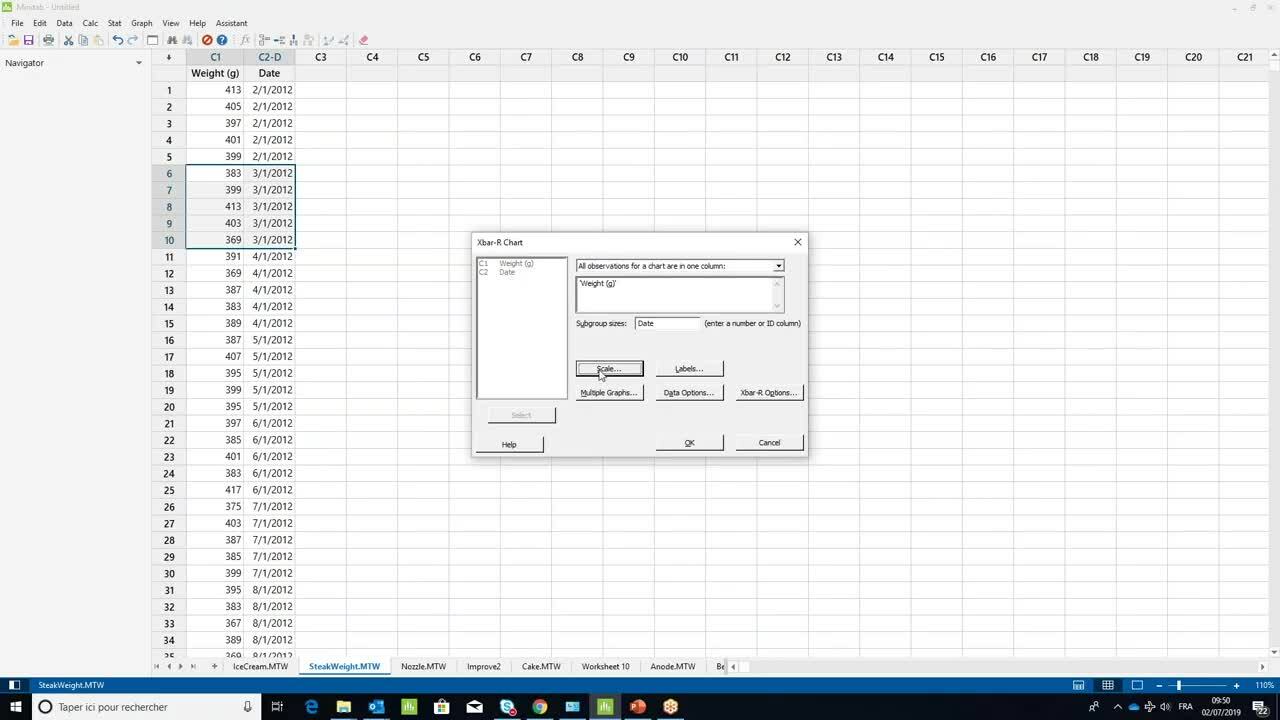
How to create an X-bar control chart ›
1:26
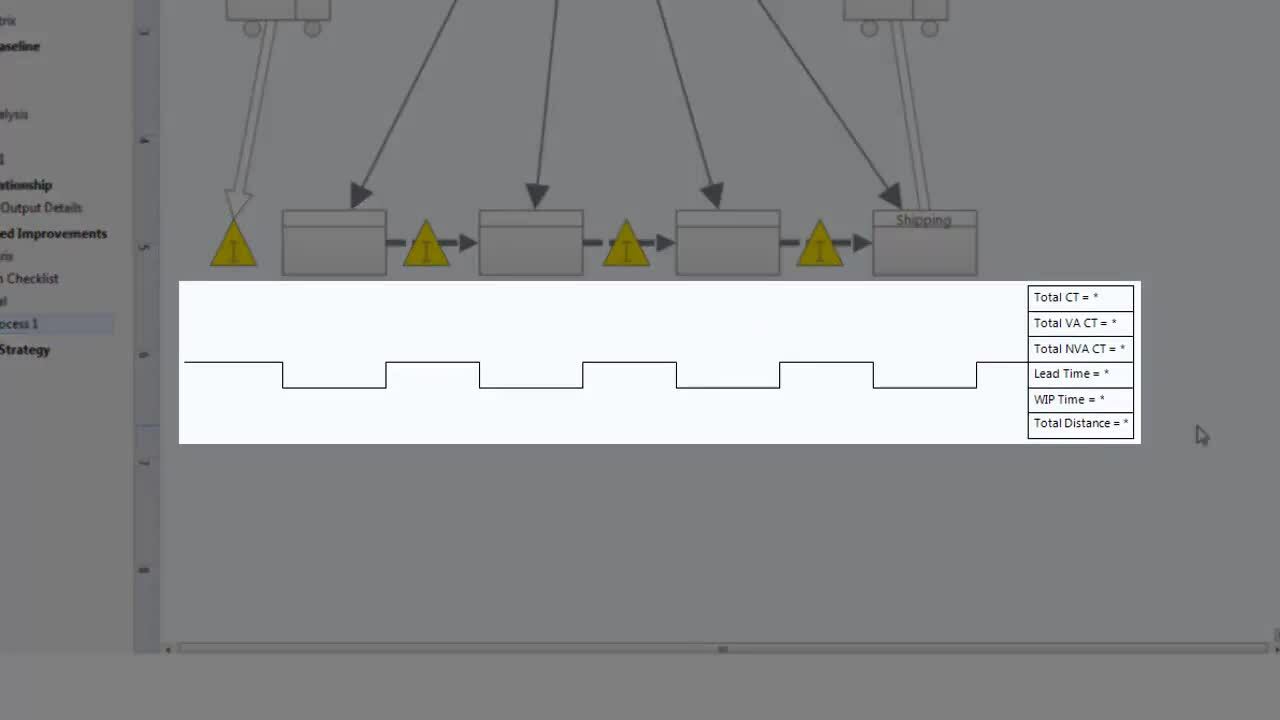
Using Value Stream Maps ›
3:54
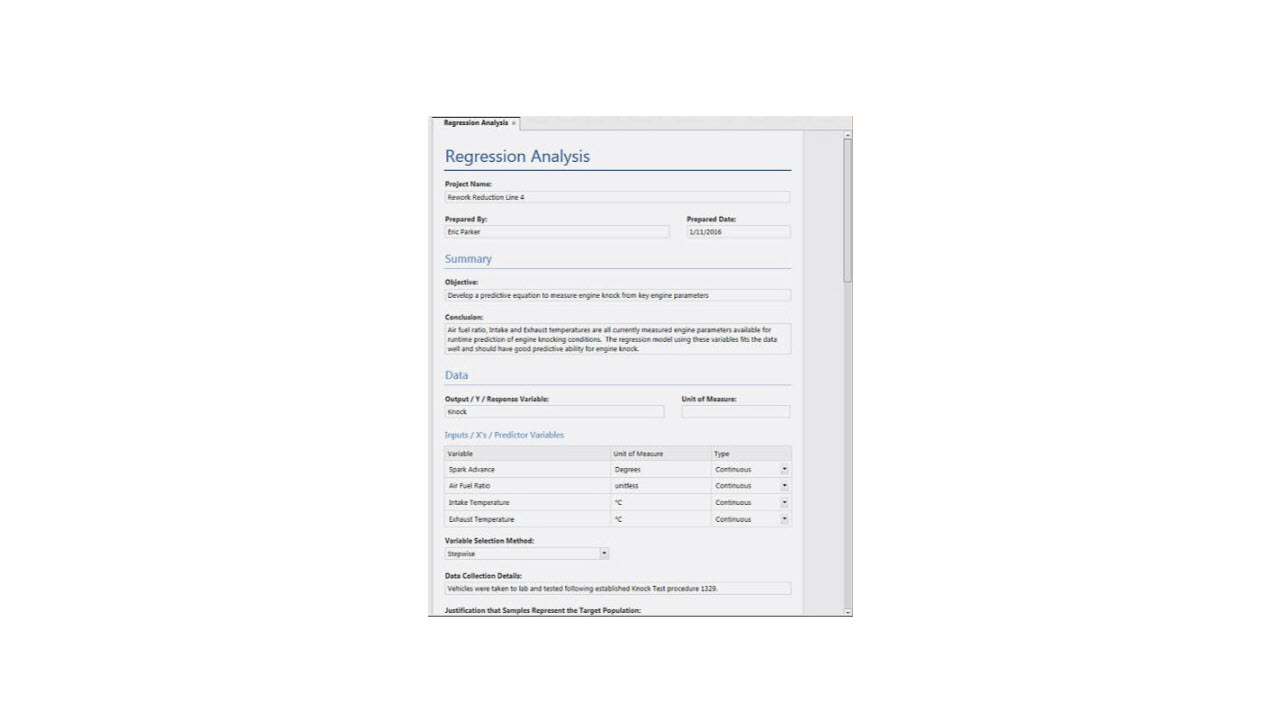
Using Analysis Capture Tools ›
1:26
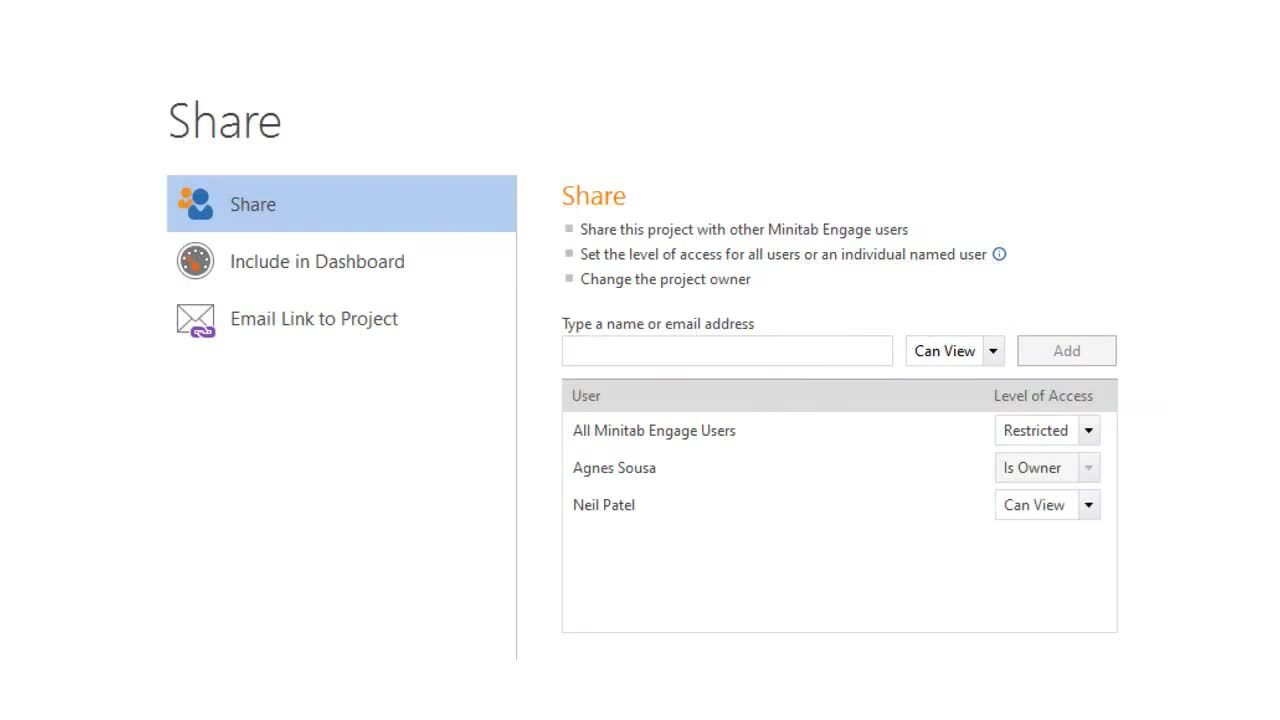
Working with Projects ›
3:47
Additional Resources
Discover use cases, tips, techniques, and product features to accelerate your analytics journey.

Blog Article
Accelerate Idea Generation, Innovation and Business Transformation with Minitab Engage ›
Additional Minitab Support
Training
Explore training options, upcoming courses, learning paths, and more.
Resources
Access additional resources to learn how Minitab can work for you.













