Sigma (σ) is the standard deviation of the process. If you enter an historical value for σ, then Minitab uses the historical value. Otherwise, Minitab uses one of the following methods to estimate σ from the data.
In This Topic
Rbar method
Minitab uses the range of each subgroup, 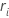 , to calculate
, to calculate 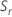 , which is an unbiased estimator of σ:
, which is an unbiased estimator of σ:
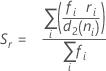
where
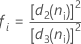
When the subgroup size is constant, the formula simplifies to the following:
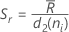
where 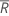 (Rbar) is the mean of the subgroup ranges, calculated as follows:
(Rbar) is the mean of the subgroup ranges, calculated as follows:

Notation
| Term | Description |
|---|---|
| ri | range for subgroup i |
| m | number of subgroups |
| d2(·) | value of unbiasing constant d2 that corresponds to the value specified in parentheses. |
| ni | number of observations in subgroup i |
| d3(·) | value of unbiasing constant d3 that corresponds to the value specified in parentheses. |
Pooled standard deviation method
The pooled standard deviation (Sp) is given by the following formula:
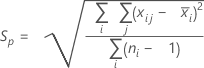
When the subgroup size is constant, Sp can also be calculated as follows:

With unbiasing constant
By default, Minitab applies the unbiasing constant, c4(), when you use the pooled standard deviation to estimate σ:
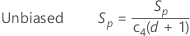
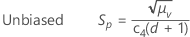
Notation
| Term | Description |
|---|---|
| xij | jth observation in the ith subgroup |
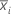 | mean of subgroup i |
| ni | number of observations in subgroup i |
| μv | mean of the subgroup variances |
| c4(·) | value of the unbiasing constant c4 that corresponds to the value that is specified in parentheses. |
| d | degrees of freedom for Sp, given by the following formula:
 |
