In This Topic
Calculating power
Calculating power
Minitab assumes that there are no text factors, and therefore no pseudo center points.
Minitab first calculates the degrees of freedom for error (v).
- Degrees of freedom for error
- ν = (total number of observations – number of parameters estimated)
- Power

Notation
| Term | Description |
|---|---|
| k | number of factors |
| r | number of runs at the corner points per replicate |
| n | number of replicates |
| b | number of blocks (if no blocking exists, b = 1)) |
| σ | estimated standard deviation |
| δ | effect |
| α | significance level |
| v | degrees of freedom for error |
| λ | noncentrality parameter |
| fα | critical value (upper α point of the F distribution with 1 and ν degrees of freedom) |
| F(fα ; 1, v, λ) | CDF of the F distribution with 1 numerator degree of freedom, v denominator degrees of freedom, and noncentrality parameter λ, evaluated at fα |
| cpblock | number of center points per block |
| cptotal | total number of center points = b * cpblock |
Calculating replicates, effects, and center points
If you provide values for power and two other properties, Minitab calculates the unknown fourth property by applying the power equation iteratively. At each iteration, Minitab evaluates the power for the values of the properties that you provide and a trial value of the statistic that you did not provide. Minitab stops when the algorithm reaches the power value that you specified.
When you provide a power value, Minitab may find that no integer number of replicates yields your target power. In such cases, Minitab displays the target value for power alongside the actual power attainable given your specifications. The actual power is a value nearest to, yet greater than, the target power.
Noncentrality parameter
Formula
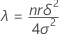
Notation
| Term | Description |
|---|---|
| r | number of runs at the corner points per replicate |
| n | number of replicates |
| σ | estimated standard deviation |
| δ | effect |
| λ | noncentrality parameter |
