Plotted points
Each point on a Laney P' chart represents the proportion of defective items or units for one subgroup.
Interpretation
If the process is in control, the points vary randomly around the center line, and the process exhibits only common-cause variation. Investigate points that fall outside the control limits or that exhibit nonrandom patterns for possible special-cause variation.
Center line
The center line on a Laney P' chart represents the average proportion of defective units for the process. The average proportion of defective units is also called the process proportion.
Interpretation
Use the center line to observe how the process performs compared to the average. If the process is in control, then the points vary randomly around the center line.
CAUTION
Do not confuse the center line with the target value for your process. The target is your desired outcome. The center line is the actual outcome.
Control limits
CAUTION
Do not confuse control limits with specification limits. Specification limits represent customer requirements and indicate the amount of variation that you want to see in the process. Control limits represent the actual amount of variation that is in the sample data. A process can be in control, yet not be capable of meeting specifications.
Sigma Z
Sigma Z measures overdispersion or underdispersion in your data.
Interpretation
- A Sigma Z value of 1 indicates that no adjustment is necessary. In this case, the control limits on the Laney P' chart are exactly the same as the control limits on a traditional P chart.
- A Sigma Z value that is greater than 1 indicates that the control limits on the Laney P' chart are wider than the control limits on a traditional P chart to adjust for overdispersion.
- A Sigma Z value that is less than 1 indicates that the control limits on the Laney P' chart are narrower than the control limits on a traditional P chart to adjust for underdispersion.
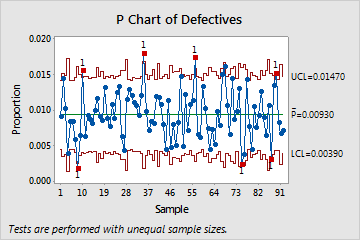
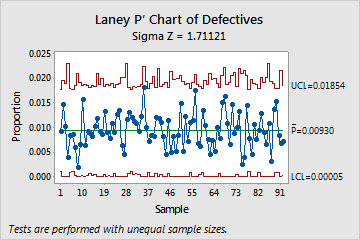
For example, the following graphs show a traditional P chart and a Laney P' chart of the same data. The subgroups are large and the data exhibit overdispersion.
- Traditional P chart
- On the traditional P chart, the large subgroup sizes result in narrow control limits. The narrow control limits and the overdispersion cause several of the subgroups to appear out of control.
- Laney P' chart
- The control limits on the Laney P' chart are adjusted for overdispersion. The Laney P' chart shows that the process is actually in control. No points fall outside of the control limits.
Tests for special causes
The tests for special causes assess whether the plotted points are randomly distributed within the control limits.
Interpretation
Use the tests for special causes to determine which observations you may need to investigate and to identify specific patterns and trends in your data. Each of the tests for special causes detects a specific pattern or trend in your data, which reveals a different aspect of process instability. For example, Test 1 detects a single out-of-control point. Test 2 detects a possible shift in the process.
Four tests are available with this control chart.
- Test 1: One point more than 3σ from center line
- Test 1 identifies subgroups that are unusual compared to other subgroups. Test 1 is universally recognized as necessary for detecting out-of-control situations. If small shifts in the process are of interest, you can use Test 2 to supplement Test 1 in order to create a control chart that has greater sensitivity.
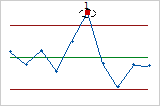
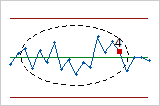
- Test 2: Nine points in a row on the same side of the center line
- Test 2 identifies shifts in the proportion of defectives for the process. If small shifts in the process are of interest, you can use Test 2 to supplement Test 1 in order to create a control chart that has greater sensitivity.
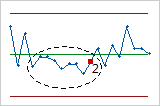
- Test 3: Six points in a row, all increasing or all decreasing
- Test 3 detects trends. This test looks for a long series of consecutive points that consistently increase in value or decrease in value.
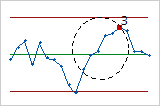
- Test 4: Fourteen points in a row, alternating up and down
- Test 4 detects systematic variation. You want the pattern of variation in a process to be random, but a point that fails Test 4 might indicate that the pattern of variation is predictable.
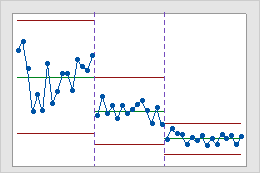
Stages
Use stages to create a historical control chart that shows how a process changes over specific periods of time. By default, Minitab recalculates the center line and control limits for each stage. For more information, go to Add stages to show how a process changed.
Interpretation
This historical control chart shows three stages of a process, which represent before, during, and after the implementation of a new procedure.