In This Topic
Estimating standard deviation
Normal capability analysis estimates within-subgroup standard deviation and overall standard deviation.
Within-subgroup standard deviation
The method used to estimate σwithin depends on the subgroup size.
- Pooled standard deviation:

where:
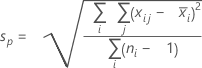
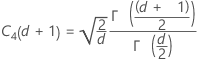
Note
If you change the default method and choose not to use the unbiasing constant, σwithin is estimated by Sp.
Term Description d Degrees of freedom for Sp= Σ (ni- 1) Xij jth observation in the ith subgroup X̅i Mean of the ith subgroup ni Number of observations in the ith subgroup C4(d+1) Unbiasing constant Γ(·) Gamma function - Average of subgroup ranges
(Rbar):

where:
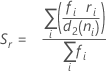
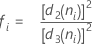
If n are all the same:
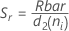
Term Description ri Range of the ith subgroup d2 (ni) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4()) d3 (ni) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4()) ni Number of observations in the ith subgroup - Average of subgroup standard
deviations (Sbar):

where:
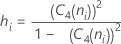
Note
If you change the default setting and do not use the unbiasing constant, σwithin is estimated by Σ Si / number of subgroups.
Term Description C4(ni) Unbiasing constant (as defined for pooled standard deviation) Si Standard deviation of subgroup i ni Number of observations in the ith subgroup
- Average of moving range:

where:

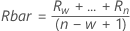
Term Description Ri The ith moving range w The number of observations used in the moving range. The default is w = 2 d2(w) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4()) - Median of moving range:
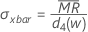
where:

Term Description MRi The ith moving range MRbar̅ Median of the MRi w The number of observations used in the moving range. The default is w = 2 d4(w) An unbiasing constant read from a table (for more information, see the section Unbiasing constants d2(), d3(), and d4()) - Square root of mean squared
successive differences (MSSD):
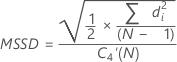
Note
If you change the default setting and do not use the unbiasing constant, σwithin is estimated by

Term Description di Successive differences C4(ni) Unbiasing constant (as defined for the pooled standard deviation) C4'(ni) Unbiasing constant ≈ c4(ni) (for more information, see the section Unbiasing constant c4'()) N Total number of observations ni Number of observations in the ith subgroup
Overall standard deviation

where:
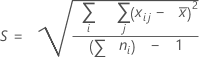
Note
By default, Minitab does not use the unbiasing constant when estimating σoverall. σoverall is estimated by S. If you want to estimate overall standard deviation using the unbiasing constant, you can change this option on the Estimate subdialog box when you perform the capability analysis. If you always want Minitab to use the unbiasing constant by default, choose and select the appropriate options.
| Term | Description |
|---|---|
| xij | The jth observation in the ith subgroup |
| x̅ | Process mean |
| ni | Number of observations in the ith subgroup |
| C4 (N) | Unbiasing constant (as defined for the pooled standard deviation) |
| N (or Σ ni) | Total number of observations |
Box-Cox transformation
The Box-Cox transformation estimates a lambda value, as shown in the following table, which minimizes the standard deviation of a standardized transformed variable. The resulting transformation is Yλ when λ ҂ 0 and ln Y when λ = 0.
The Box-Cox method searches through many types of transformations. The following table shows some common transformations where Y' is the transform of the data Y.
| Lambda (λ) value | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
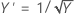 |
 |
 |
Algorithm for Johnson transformation
The Johnson transformation optimally selects one of three families of distribution to transform the data to follow a normal distribution.
| Johnson family | Transformation function | Range |
|---|---|---|
| SB | γ + η ln [(x – ε) / (λ + ε – x)] | η, λ > 0, –∞ < γ < ∞ , –∞ < ε < ∞, ε < x < ε + λ |
| SL | γ + η ln (x – ε) | η > 0, –∞ < γ < ∞, –∞ < ε < ∞, ε < x |
| SU | γ + η Sinh–1 [(x – ε) / λ] , where
Sinh–1(x) = ln [x + sqrt (1 + x2)] |
η, λ > 0, –∞ < γ < ∞, –∞ < ε < ∞, –∞ < x < ∞ |
The algorithm uses the following procedure:
- Considers almost all potential transformation functions from the Johnson system.
- Estimates the parameters in the function using the method described in Chou, et al.1
- Transforms the data using the transformation function.
- Calculates Anderson-Darling statistics and the corresponding p-value for the transformed data.
- Selects the transformation function that has the largest p-value that is greater than the p-value criterion (default is 0.10) that you specify in the Transform dialog box. Otherwise, no transformation is appropriate.
Notation
| Term | Description |
|---|---|
| SB | The Johnson family distribution with the variable bounded (B) |
| SL | The Johnson family distribution with the variable lognormal (L) |
| SU | The Johnson family distribution with the variable unbounded (U) |
For more information on the Johnson transformation, see Chou, et al.1 Minitab replaces the Shapiro-Wilks normality test used in that text with the Anderson-Darling test.
For information on the probability plot, percentiles, and their confidence intervals, go to Methods and formulas for distributions in Individual Distribution Identification.
Unbiasing constants d2(), d3(), and d4()
d2(N) is the expected value of the range of N observations from a normal population with standard deviation = 1. Thus, if r is the range of a sample of N observations from a normal distribution with standard deviation = σ, then E(r) = d2(N)σ.
d3(N) is the standard deviation of the range of N observations from a normal population with σ = 1. Thus, if r is the range of a sample of N observations from a normal distribution with standard deviation = σ, then stdev(r) = d3(N)σ.
Use the following table to find an unbiasing constant for a given value, N. (To determine the value of N, consult the formula for the statistic of interest.)

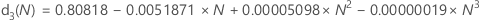
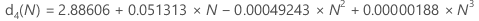
- D. J. Wheeler and D. S. Chambers. (1992). Understanding Statistical Process Control, Second Edition, SPC Press, Inc.
- H. Leon Harter (1960). "Tables of Range and Studentized Range". The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1.128 | 0.8525 | 0.954 |
| 3 | 1.693 | 0.8884 | 1.588 |
| 4 | 2.059 | 0.8798 | 1.978 |
| 5 | 2.326 | 0.8641 | 2.257 |
| 6 | 2.534 | 0.8480 | 2.472 |
| 7 | 2.704 | 0.8332 | 2.645 |
| 8 | 2.847 | 0.8198 | 2.791 |
| 9 | 2.970 | 0.8078 | 2.915 |
| 10 | 3.078 | 0.7971 | 3.024 |
| 11 | 3.173 | 0.7873 | 3.121 |
| 12 | 3.258 | 0.7785 | 3.207 |
| 13 | 3.336 | 0.7704 | 3.285 |
| 14 | 3.407 | 0.7630 | 3.356 |
| 15 | 3.472 | 0.7562 | 3.422 |
| 16 | 3.532 | 0.7499 | 3.482 |
| 17 | 3.588 | 0.7441 | 3.538 |
| 18 | 3.640 | 0.7386 | 3.591 |
| 19 | 3.689 | 0.7335 | 3.640 |
| 20 | 3.735 | 0.7287 | 3.686 |
| 21 | 3.778 | 0.7242 | 3.730 |
| 22 | 3.819 | 0.7199 | 3.771 |
| 23 | 3.858 | 0.7159 | 3.811 |
| 24 | 3.895 | 0.7121 | 3.847 |
| 25 | 3.931 | 0.7084 | 3.883 |
| N | d2(N) |
|---|---|
| 26 | 3.964 |
| 27 | 3.997 |
| 28 | 4.027 |
| 29 | 4.057 |
| 30 | 4.086 |
| 31 | 4.113 |
| 32 | 4.139 |
| 33 | 4.165 |
| 34 | 4.189 |
| 35 | 4.213 |
| 36 | 4.236 |
| 37 | 4.259 |
| 38 | 4.280 |
| 39 | 4.301 |
| 40 | 4.322 |
| 41 | 4.341 |
| 42 | 4.361 |
| 43 | 4.379 |
| 44 | 4.398 |
| 45 | 4.415 |
| 46 | 4.433 |
| 47 | 4.450 |
| 48 | 4.466 |
| 49 | 4.482 |
| 50 | 4.498 |
Unbiasing constants c4() and c5()
c4()

c5()

Notation
| Term | Description |
|---|---|
| Γ() | gamma function |
Unbiasing constant c4'()
Use the following tables to find values for the unbiasing constant, c4'(), which is used in the formulas for the square root of MSSD method of estimating sigma.
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 2 | 0.797850 | 41 | 0.990797 | 80 | 0.995215 |
| 3 | 0.871530 | 42 | 0.991013 | 81 | 0.995272 |
| 4 | 0.905763 | 43 | 0.991218 | 82 | 0.995328 |
| 5 | 0.925222 | 44 | 0.991415 | 83 | 0.995383 |
| 6 | 0.937892 | 45 | 0.991602 | 84 | 0.995436 |
| 7 | 0.946837 | 46 | 0.991782 | 85 | 0.995489 |
| 8 | 0.953503 | 47 | 0.991953 | 86 | 0.995539 |
| 9 | 0.958669 | 48 | 0.992118 | 87 | 0.995589 |
| 10 | 0.962793 | 49 | 0.992276 | 88 | 0.995638 |
| 11 | 0.966163 | 50 | 0.992427 | 89 | 0.995685 |
| 12 | 0.968968 | 51 | 0.992573 | 90 | 0.995732 |
| 13 | 0.971341 | 52 | 0.992713 | 91 | 0.995777 |
| 14 | 0.973375 | 53 | 0.992848 | 92 | 0.995822 |
| 15 | 0.975137 | 54 | 0.992978 | 93 | 0.995865 |
| 16 | 0.976679 | 55 | 0.993103 | 94 | 0.995908 |
| 17 | 0.978039 | 56 | 0.993224 | 95 | 0.995949 |
| 18 | 0.979249 | 57 | 0.993340 | 96 | 0.995990 |
| 19 | 0.980331 | 58 | 0.993452 | 97 | 0.996030 |
| 20 | 0.981305 | 59 | 0.993561 | 98 | 0.996069 |
| 21 | 0.982187 | 60 | 0.993666 | 99 | 0.996108 |
| 22 | 0.982988 | 61 | 0.993767 | 100 | 0.996145 |
| 23 | 0.983720 | 62 | 0.993866 | 101 | 0.996182 |
| 24 | 0.984391 | 63 | 0.993961 | 102 | 0.996218 |
| 25 | 0.985009 | 64 | 0.994053 | 103 | 0.996253 |
| 26 | 0.985579 | 65 | 0.994142 | 104 | 0.996288 |
| 27 | 0.986107 | 66 | 0.994229 | 105 | 0.996322 |
| 28 | 0.986597 | 67 | 0.994313 | 106 | 0.996356 |
| 29 | 0.987054 | 68 | 0.994395 | 107 | 0.996389 |
| 30 | 0.987480 | 69 | 0.994474 | 108 | 0.996421 |
| 31 | 0.987878 | 70 | 0.994551 | 109 | 0.996452 |
| 32 | 0.988252 | 71 | 0.994626 | 110 | 0.996483 |
| 33 | 0.988603 | 72 | 0.994699 | 111 | 0.996514 |
| 34 | 0.988934 | 73 | 0.994769 | 112 | 0.996544 |
| 35 | 0.989246 | 74 | 0.994838 | 113 | 0.996573 |
| 36 | 0.989540 | 75 | 0.994905 | 114 | 0.996602 |
| 37 | 0.989819 | 76 | 0.994970 | 115 | 0.996631 |
| 38 | 0.990083 | 77 | 0.995034 | 116 | 0.996658 |
| 39 | 0.990333 | 78 | 0.995096 | 117 | 0.996686 |
| 40 | 0.990571 | 79 | 0.995156 | 118 | 0.996713 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 119 | 0.996739 | 160 | 0.997541 | 201 | 0.998016 |
| 120 | 0.996765 | 161 | 0.997555 | 202 | 0.998025 |
| 121 | 0.996791 | 162 | 0.997570 | 203 | 0.998034 |
| 122 | 0.996816 | 163 | 0.997584 | 204 | 0.998043 |
| 123 | 0.996841 | 164 | 0.997598 | 205 | 0.998052 |
| 124 | 0.996865 | 165 | 0.997612 | 206 | 0.998061 |
| 125 | 0.996889 | 166 | 0.997625 | 207 | 0.998070 |
| 126 | 0.996913 | 167 | 0.997639 | 208 | 0.998078 |
| 127 | 0.996936 | 168 | 0.997652 | 209 | 0.998087 |
| 128 | 0.996959 | 169 | 0.997665 | 210 | 0.998095 |
| 129 | 0.996982 | 170 | 0.997678 | 211 | 0.998104 |
| 130 | 0.997004 | 171 | 0.997691 | 212 | 0.998112 |
| 131 | 0.997026 | 172 | 0.997703 | 213 | 0.998120 |
| 132 | 0.997047 | 173 | 0.997716 | 214 | 0.998128 |
| 133 | 0.997069 | 174 | 0.997728 | 215 | 0.998137 |
| 134 | 0.997089 | 175 | 0.997741 | 216 | 0.998145 |
| 135 | 0.997110 | 176 | 0.997753 | 217 | 0.998152 |
| 136 | 0.997130 | 177 | 0.997765 | 218 | 0.998160 |
| 137 | 0.997150 | 178 | 0.997776 | 219 | 0.998168 |
| 138 | 0.997170 | 179 | 0.997788 | 220 | 0.998176 |
| 139 | 0.997189 | 180 | 0.997800 | 221 | 0.998184 |
| 140 | 0.997209 | 181 | 0.997811 | 222 | 0.998191 |
| 141 | 0.997227 | 182 | 0.997822 | 223 | 0.998199 |
| 142 | 0.997246 | 183 | 0.997834 | 224 | 0.998206 |
| 143 | 0.997264 | 184 | 0.997845 | 225 | 0.998214 |
| 144 | 0.997282 | 185 | 0.997856 | 226 | 0.998221 |
| 145 | 0.997300 | 186 | 0.997866 | 227 | 0.998228 |
| 146 | 0.997318 | 187 | 0.997877 | 228 | 0.998235 |
| 147 | 0.997335 | 188 | 0.997888 | 229 | 0.998242 |
| 148 | 0.997352 | 189 | 0.997898 | 230 | 0.998250 |
| 149 | 0.997369 | 190 | 0.997909 | 231 | 0.998257 |
| 150 | 0.997386 | 191 | 0.997919 | 232 | 0.998263 |
| 151 | 0.997402 | 192 | 0.997929 | 233 | 0.998270 |
| 152 | 0.997419 | 193 | 0.997939 | 234 | 0.998277 |
| 153 | 0.997435 | 194 | 0.997949 | 235 | 0.998284 |
| 154 | 0.997450 | 195 | 0.997959 | 236 | 0.998291 |
| 155 | 0.997466 | 196 | 0.997969 | 237 | 0.998297 |
| 156 | 0.997481 | 197 | 0.997978 | 238 | 0.998304 |
| 157 | 0.997497 | 198 | 0.997988 | 239 | 0.998311 |
| 158 | 0.997512 | 199 | 0.997997 | 240 | 0.998317 |
| 159 | 0.997526 | 200 | 0.998007 | 241 | 0.998323 |
| N | c4'(N) | N | c4'(N) | N | c4'(N) |
|---|---|---|---|---|---|
| 242 | 0.998330 | 283 | 0.998553 | 324 | 0.998720 |
| 243 | 0.998336 | 284 | 0.998558 | 325 | 0.998723 |
| 244 | 0.998342 | 285 | 0.998562 | 326 | 0.998727 |
| 245 | 0.998349 | 286 | 0.998567 | 327 | 0.998730 |
| 246 | 0.998355 | 287 | 0.998571 | 328 | 0.998734 |
| 247 | 0.998361 | 288 | 0.998576 | 329 | 0.998737 |
| 248 | 0.998367 | 289 | 0.998580 | 330 | 0.998740 |
| 249 | 0.998373 | 290 | 0.998585 | 331 | 0.998744 |
| 250 | 0.998379 | 291 | 0.998589 | 332 | 0.998747 |
| 251 | 0.998385 | 292 | 0.998593 | 333 | 0.998751 |
| 252 | 0.998391 | 293 | 0.998598 | 334 | 0.998754 |
| 253 | 0.998397 | 294 | 0.998602 | 335 | 0.998757 |
| 254 | 0.998403 | 295 | 0.998606 | 336 | 0.998761 |
| 255 | 0.998408 | 296 | 0.998611 | 337 | 0.998764 |
| 256 | 0.998414 | 297 | 0.998615 | 338 | 0.998767 |
| 257 | 0.998420 | 298 | 0.998619 | 339 | 0.998770 |
| 258 | 0.998425 | 299 | 0.998623 | 340 | 0.998774 |
| 259 | 0.998431 | 300 | 0.998627 | 341 | 0.998777 |
| 260 | 0.998436 | 301 | 0.998632 | 342 | 0.998780 |
| 261 | 0.998442 | 302 | 0.998636 | 343 | 0.998783 |
| 262 | 0.998447 | 303 | 0.998640 | 344 | 0.998786 |
| 263 | 0.998453 | 304 | 0.998644 | 345 | 0.998790 |
| 264 | 0.998458 | 305 | 0.998648 | 346 | 0.998793 |
| 265 | 0.998463 | 306 | 0.998652 | 347 | 0.998796 |
| 266 | 0.998469 | 307 | 0.998656 | 348 | 0.998799 |
| 267 | 0.998474 | 308 | 0.998660 | 349 | 0.998802 |
| 268 | 0.998479 | 309 | 0.998664 | 350 | 0.998805 |
| 269 | 0.998484 | 310 | 0.998668 | 351 | 0.998808 |
| 270 | 0.998489 | 311 | 0.998671 | 352 | 0.998811 |
| 271 | 0.998495 | 312 | 0.998675 | 353 | 0.998814 |
| 272 | 0.998500 | 313 | 0.998679 | 354 | 0.998817 |
| 273 | 0.998505 | 314 | 0.998683 | 355 | 0.998820 |
| 274 | 0.998510 | 315 | 0.998687 | 356 | 0.998823 |
| 275 | 0.998515 | 316 | 0.998690 | 357 | 0.998826 |
| 276 | 0.998519 | 317 | 0.998694 | 358 | 0.998829 |
| 277 | 0.998524 | 318 | 0.998698 | 359 | 0.998832 |
| 278 | 0.998529 | 319 | 0.998701 | 360 | 0.998835 |
| 279 | 0.998534 | 320 | 0.998705 | 361 | 0.998837 |
| 280 | 0.998539 | 321 | 0.998709 | 362 | 0.998840 |
| 281 | 0.998544 | 322 | 0.998712 | 363 | 0.998843 |
| 282 | 0.998548 | 323 | 0.998716 | 364 | 0.998846 |
| k | c4'(k) | k | c4'(k) | k | c4'(k) |
|---|---|---|---|---|---|
| 365 | 0.998849 | 411 | 0.998963 | 457 | 0.999054 |
| 366 | 0.998851 | 412 | 0.998965 | 458 | 0.999056 |
| 367 | 0.998854 | 413 | 0.998967 | 459 | 0.999058 |
| 368 | 0.998857 | 414 | 0.998970 | 460 | 0.999060 |
| 369 | 0.998860 | 415 | 0.998972 | 461 | 0.999061 |
| 370 | 0.998862 | 416 | 0.998974 | 462 | 0.999063 |
| 371 | 0.998865 | 417 | 0.998976 | 463 | 0.999065 |
| 372 | 0.998868 | 418 | 0.998978 | 464 | 0.999067 |
| 373 | 0.998871 | 419 | 0.998980 | 465 | 0.999068 |
| 374 | 0.998873 | 420 | 0.998982 | 466 | 0.999070 |
| 375 | 0.998876 | 421 | 0.998985 | 467 | 0.999072 |
| 376 | 0.998879 | 422 | 0.998987 | 468 | 0.999073 |
| 377 | 0.998881 | 423 | 0.998989 | 469 | 0.999075 |
| 378 | 0.998884 | 424 | 0.998991 | 470 | 0.999077 |
| 379 | 0.998886 | 425 | 0.998993 | 471 | 0.999078 |
| 380 | 0.998889 | 426 | 0.998995 | 472 | 0.999080 |
| 381 | 0.998892 | 427 | 0.998997 | 473 | 0.999082 |
| 382 | 0.998894 | 428 | 0.998999 | 474 | 0.999084 |
| 383 | 0.998897 | 429 | 0.999001 | 475 | 0.999085 |
| 384 | 0.998899 | 430 | 0.999003 | 476 | 0.999087 |
| 385 | 0.998902 | 431 | 0.999005 | 477 | 0.999088 |
| 386 | 0.998904 | 432 | 0.999007 | 478 | 0.999090 |
| 387 | 0.998907 | 433 | 0.999009 | 479 | 0.999092 |
| 388 | 0.998909 | 434 | 0.999011 | 480 | 0.999093 |
| 389 | 0.998912 | 435 | 0.999013 | 481 | 0.999095 |
| 390 | 0.998914 | 436 | 0.999015 | 482 | 0.999097 |
| 391 | 0.998917 | 437 | 0.999017 | 483 | 0.999098 |
| 392 | 0.998919 | 438 | 0.999019 | 484 | 0.999100 |
| 393 | 0.998921 | 439 | 0.999021 | 485 | 0.999101 |
| 394 | 0.998924 | 440 | 0.999023 | 486 | 0.999103 |
| 395 | 0.998926 | 441 | 0.999025 | 487 | 0.999104 |
| 396 | 0.998929 | 442 | 0.999027 | 488 | 0.999106 |
| 397 | 0.998931 | 443 | 0.999028 | 489 | 0.999108 |
| 398 | 0.998933 | 444 | 0.999030 | 490 | 0.999109 |
| 399 | 0.998936 | 445 | 0.999032 | 491 | 0.999111 |
| 400 | 0.998938 | 446 | 0.999034 | 492 | 0.999112 |
| 401 | 0.998940 | 447 | 0.999036 | 493 | 0.999114 |
| 402 | 0.998943 | 448 | 0.999038 | 494 | 0.999115 |
| 403 | 0.998945 | 449 | 0.999040 | 495 | 0.999117 |
| 404 | 0.998947 | 450 | 0.999042 | 496 | 0.999118 |
| 405 | 0.998950 | 451 | 0.999043 | 497 | 0.999120 |
| 406 | 0.998952 | 452 | 0.999045 | 498 | 0.999121 |
| 407 | 0.998954 | 453 | 0.999047 | 499 | 0.999123 |
| 408 | 0.998956 | 454 | 0.999049 | 500 | 0.999124 |
| 409 | 0.998959 | 455 | 0.999051 | ||
| 410 | 0.998961 | 456 | 0.999052 |
Gamma table
Use the table below to find a value for γN, 1 -α used in calculating the confidence interval for Z.Bench and then use the second equation to get the exact value of γN, 1 -α.
| 1 -α | |||||
| N | 0.800 | 0.850 | 0.900 | 0.950 | 0.990 |
| 5 | 3.544 | 4.138 | 4.961 | 6.350 | 9.750 |
| 6 | 3.485 | 4.078 | 4.903 | 6.300 | 9.636 |
| 7 | 3.443 | 4.035 | 4.861 | 6.260 | 9.567 |
| 8 | 3.413 | 4.003 | 4.829 | 6.229 | 9.520 |
| 9 | 3.390 | 3.979 | 4.804 | 6.204 | 9.484 |
| 10 | 3.372 | 3.960 | 4.783 | 6.183 | 9.457 |
| 12 | 3.345 | 3.931 | 4.753 | 6.152 | 9.416 |
| 14 | 3.326 | 3.911 | 4.732 | 6.130 | 9.387 |
| 16 | 3.312 | 3.986 | 4.716 | 6.113 | 9.365 |
| 18 | 3.301 | 3.884 | 4.703 | 6.099 | 9.348 |
| 20 | 3.293 | 3.875 | 4.693 | 6.089 | 9.335 |
| 25 | 3.278 | 3.858 | 4.675 | 6.069 | 9.310 |
| 30 | 3.268 | 3.848 | 4.664 | 6.056 | 9.294 |
| 35 | 3.261 | 3.840 | 4.655 | 6.047 | 9.282 |
| 40 | 3.255 | 3.834 | 4.649 | 6.040 | 9.274 |
| 50 | 3.248 | 3.826 | 4.640 | 6.031 | 9.262 |
| 60 | 3.243 | 3.821 | 4.634 | 6.024 | 9.253 |
| 80 | 3.237 | 3.814 | 4.627 | 6.016 | 9.244 |
| 100 | 3.233 | 3.810 | 4.623 | 6.011 | 9.238 |
| >100 | 3.219 | 3.794 | 4.605 | 5.991 | 9.210 |
When N and 1 - a are not listed in the table, use the extrapolation method to obtain the value for γN, 1 -α. For example,
- For a value of α between 0.05 and 0.1 (i.e. 0.95 > 1 -α > 0.90) and N = 10,

- For a value of N between 60 and 80 and α = 0.80,
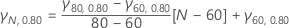
- For a value of α between 0.05 and 0.1 and a value of N between 60 and 80, use the first equation to calculate the values of γ80, 1 -α and γ60, 1 -α
