Select the method or formula of your choice.
In This Topic
Calculating power with Levene's method
The power function for a variance test is Q(ρ) = P(Reject H0 | ρ).
One-sided power (H1: σ1 / σ2 < 1
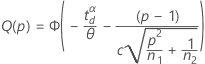
One-sided power (H1: σ1 / σ2 > 1)
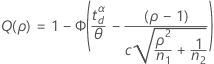
Two-sided (H1: σ1 / σ2 ≠ 1
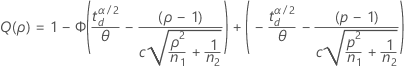
Notation
| Term | Description |
|---|---|
| Φ | CDF of the standard normal distribution |
| tα d | upper percentile of the t distribution with d = n1 + n2 – 2 degrees of freedom |
| θ | 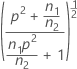 |
| c |  |
| ρ | σ 1 / σ 2 |
| n 1 | size of the first sample |
| n 2 | size of the second sample |
Calculating power with the F-test method
Formula
The power function for a variance test is Q(ρ) = P(Reject H0 | ρ).
One-sided power (H1: σ1 / σ2 < 1)
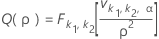
One-sided power (H1: σ1 / σ2 > 1)
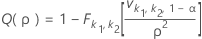
Two-sided power (H1: σ1 / σ2 ≠ 1)
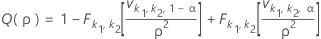
Notation
| Term | Description |
|---|---|
| F k 1, k 2 | distribution function of the F distribution with k1 and k2 degrees of freedom |
| v k 1, k 2, A | inverse CDF evaluated at A for an F distribution with k 1 and k 2 degrees of freedom |
| k 1 | n – 1 |
| k2 | n – 1 |
| α | significance level |
| ρ | σ 1 / σ 2 |
Calculating power using Bonett's method
Note
To calculate power for the Bonett method, use the session command POWER with the subcommands TWOVARIANCE and BONETT.
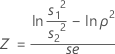

One-sided power (H1: σ1 / σ2 < 1)
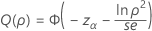
One-sided power (H1: σ1 / σ2 > 1)
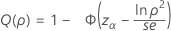
One-sided power (H1: σ1 / σ2 ≠ 1)

Notation
| Term | Description |
|---|---|
| Si | the standard deviation of sample i |
| ρ | the ratio of the population standard deviations ( s1 / s2) |
| se | the standard error |
| γ | the true common kurtosis of the parent populations (γ is not the excess kurtosis) |
| n | the sample size (For power calculations, n is assumed to be the same for both samples) |
| Φ | the cumulative distribution function for the standard normal distribution |
| α | the significance level for the test |
| zi | the upper i percentile point for the standard normal distribution |
Calculating sample size and ratio
If you provide values for power and sample size, Minitab calculates the value of the ratio. If you provide values for power and ratio, Minitab calculates the value of the sample size.
For these two cases, Minitab uses an iterative algorithm with the power equation. At each iteration, Minitab evaluates the power for a trial sample size or trial ratio, and stops when it reaches the values you request.
Target power and actual power
When Minitab calculates sample size, it may find that no integer value of sample size yields your target power. In such cases, Minitab displays the target value for power alongside the actual power, which is a value corresponding to an integer sample size, and which is nearest to, yet greater than, the target value.
