A quality analyst wants to determine whether the mean amount of active ingredient in a generic brand of pain reliever is within 1 mg of the mean amount in a popular brand of pain reliever. Before collecting the data for a 2-sample equivalence test, the analyst uses a power and sample size calculation to determine how large the sample must be to obtain a power of 90% (0.9). From previous samples, the analyst estimates the standard deviation of the population is 0.41.
- Choose .
- From Hypothesis about, select Test mean - reference mean (Difference).
- From What do you want to determine? (Alternative hypothesis), select Lower limit < test mean - reference mean < upper limit.
- In Lower limit, enter -1. In Upper limit, enter 1.
- In Differences (within the limits), enter 0.5 0.7 0.9.
- In Power values, enter 0.9.
- In Standard deviation, enter 0.41.
- Click OK.
Interpret the results
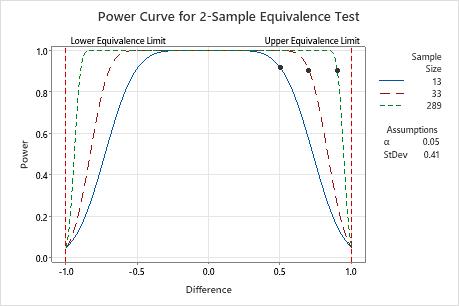
If the difference is 0.5, then the analyst needs 13 observations in each group to achieve a power of at least 0.9. If the analyst uses a sample size of 13, the power of the test is approximately 0.92.
When the difference is closer to the lower equivalence limit (–1) or the upper equivalence limit (1), then the analyst needs a larger sample size to achieve the same power. For example, for a difference of 0.9, the analyst needs a sample size of at least 289 observations in each group to achieve a power of 0.9.
For any sample size, as the difference approaches the lower equivalence limit or the upper equivalence limit, the power of the test decreases and approaches α (alpha, which is the risk of claiming equivalence when it is not true).
Method
| Power for difference: | Test mean - reference mean |
|---|---|
| Null hypothesis: | Difference ≤ -1 or Difference ≥ 1 |
| Alternative hypothesis: | -1 < Difference < 1 |
| α level: | 0.05 |
| Assumed standard deviation: | 0.41 |
Results
| Difference | Sample Size | Target Power | Actual Power |
|---|---|---|---|
| 0.5 | 13 | 0.9 | 0.915407 |
| 0.7 | 33 | 0.9 | 0.902461 |
| 0.9 | 289 | 0.9 | 0.900360 |