In This Topic
Observed number of runs
The observed number of runs is the number of groups of observations that are above or below the comparison criterion, K. Minitab uses the comparison criteria as a value you specify or the default mean of the observations. The number of runs in the sample helps determine whether the sample is random.
For example, a die is rolled 25 times. The scores are as follows:
- 4 6 3 2 2 1 6 4 4 5 1 1 4 5 3 1 5 6 6 3 4 4 5 2 3
Let the comparison criteria K = 3.5. The runs are as follows:
- (4 6) (3 2 2 1) (6 4 4 5) (1 1) (4 5) (3 1) (5 6 6) (3) (4 4 5) (2 3)
The first run (4 6) has values that are above K = 3.5, the second run (3 2 2 1) has values that are below K, and so on.
The observed number of runs = 10.
Test statistics
Formula

The p-value is the probability of observing the absolute value of a standard normal variable that is greater than the absolute value of Z.
If too few observations exist for the normal approximation to be valid, Minitab displays a message. Exact tables are widely available.
Notation
| Term | Description |
|---|---|
| Observed | The number of runs in the sample |
| Expected |
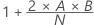 |
| Variance |
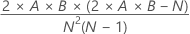 |
| A | The number of observations above K |
| B | The number of observations below or equal to K |
| N | The number of observations |
