In This Topic
Difference

Notation
| Term | Description |
|---|---|
| D | Difference |
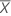 | Test mean |
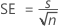
Standard error of the difference (SE)
Notation
| Term | Description |
|---|---|
| s | Standard deviation of the observations |
| n | Number of observations |
Equivalence limits



Degrees of freedom (DF)

Notation
| Term | Description |
|---|---|
| v | Degrees of freedom |
| n | Number of observations |
Confidence interval for the difference
100(1 – α)% CI
By default, Minitab uses the following formula to calculate the 100(1 – α)% confidence interval (CI) for the difference:
CI = [min(C, Dl), max(C, Du)]
where:

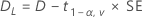
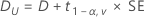
100(1 – 2α)% CI
If you select the option to use the 100(1 – 2 α)% CI, then the CI is given by the following formula:
CI = [Dl, Du]
One-sided intervals
For a hypotheses of Test mean > target, or Test mean - target > lower limit, the 100(1 – α)% lower bound is equal to DL.
For a hypothesis of Test mean < target, or Test mean - target < upper limit, the 100(1 – α)% upper bound is equal to DU.
Notation
| Term | Description |
|---|---|
| D | Difference between the mean of the test sample and the target value |
| SE | Standard error |
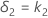
| δ1 | Lower equivalence limit |
| δ2 | Upper equivalence limit |
| v | Degrees of freedom |
| α | Significance level for the test |
| t1 – α, v | Upper 1 – α critical value for a t-distribution with v degrees of freedom |
T-values
 , and let t 2 be the t-value for the hypothesis,
, and let t 2 be the t-value for the hypothesis,  , where
, where  is the difference between the mean of the test population and the target value. By default, the t-values are calculated as follows:
is the difference between the mean of the test population and the target value. By default, the t-values are calculated as follows:


For a hypothesis of Test mean > target, δ1= 0.
For a hypothesis of Test mean < target, δ2= 0.
Notation
| Term | Description |
|---|---|
| D | Difference between the mean of the test sample and the target value |
| SE | Standard error of the difference |
| δ1 | Lower equivalence limit |
| δ2 | Upper equivalence limit |
P-values
The probability, PH0, for each null hypothesis (H0) is given by the following:
| H0 | P-Value |
|---|---|
 |
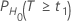 |
 |
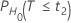 |
Notation
| Term | Description |
|---|---|
 | Unknown difference between the mean of the test population and the target value |
| δ1 | Lower equivalence limit |
| δ2 | Upper equivalence limit |
| v | Degrees of freedom |
| T | t distribution with v degrees of freedom |
| t1 | The t-value for the hypothesis  |
| t2 | The t- value for the hypothesis  |
Note
For information on how the t-values are calculated, see the section on t-values.
