A quality engineer for a nutritional supplement company wants to assess the calcium content in vitamin capsules. The engineer collects a random sample of capsules and records their calcium content. To determine which statistical analysis is appropriate for the data, the engineer first needs to determine the data distribution.
The engineer performs individual distribution identification to determine which distribution best fits the data.
- Open the sample data, CalciumContent.MTW.
- Choose .
- In Data are arranged as, select Single column, then enter Calcium.
- In Subgroup size, enter 1.
- Click OK.
Interpret the results
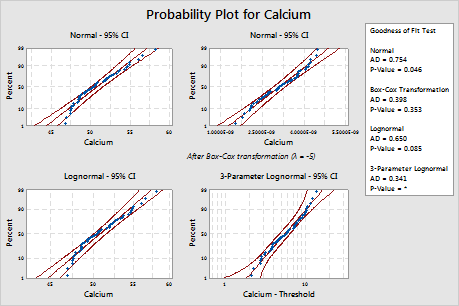
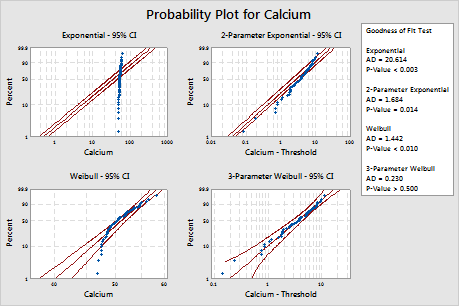
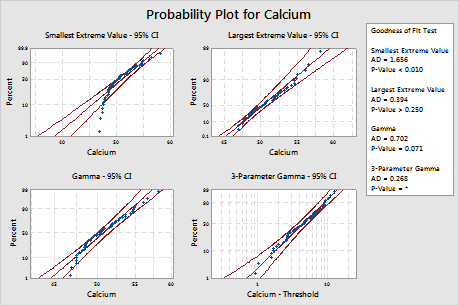
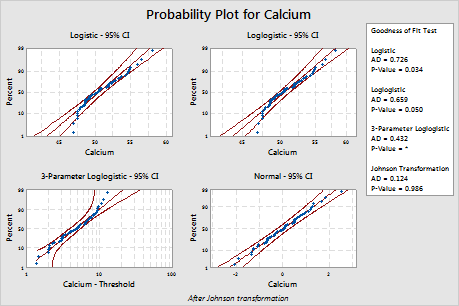
Minitab displays a probability plot and a p-value for each distribution and transformation. If a distribution is a good fit for the data (or if a transformation is effective), the points on the plot follow a straight line within the confidence bounds and the p-value is greater than the alpha level. An alpha level of 0.05 is often used. The p-value for the likelihood-ratio test (LRT) indicates whether adding an additional parameter to a distribution significantly improves its fit. An LRT p-value that is less than 0.05 suggests that the improvement is significant.
For these data, the 3-parameter Weibull distribution (p > 0.500) and the largest extreme value distribution (p > 0.250) are a good fit for the data. Adding a third parameter significantly improves the fit of the lognormal distribution (LRT P = 0.017), the Weibull distribution (LRT P = 0.000), the gamma distribution (LRT P = 0.006), and the loglogistic distribution (LRT P = 0.027).
The Box-Cox transformation (p = 0.324) and the Johnson transformation (p = 0.986) are effective for these data. After the transformation, the normal distribution provides a good fit for the transformed values.
Distribution Identification for Calcium
2-Parameter Exponential
Distribution ID Plot for Calcium
Distribution ID Plot for Calcium
Distribution ID Plot for Calcium