In This Topic
U Chart
The U chart plots the number of defects (also called nonconformities) per unit. The center line is the mean number of defectives per unit (or subgroup). The control limits, which are set at a distance of 3 standard deviations above and below the center line, show the amount of variation that is expected in the subgroup means.
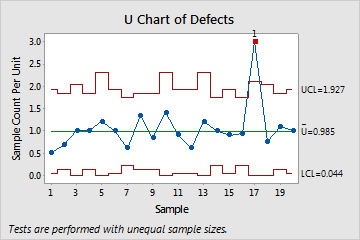
This U chart shows that, on average, the rate of defects per unit across the samples is approximately 1. One point appears out of control.
Interpretation
Use the U chart to visually monitor the defects per unit and to determine whether the defect rate is stable and in control.
Red points indicate subgroups that fail at least one of the tests for special causes and are not in control. Out-of-control points indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
Tests for special causes
The tests for special causes assess whether the plotted points on each control chart are randomly distributed within the control limits.
Interpretation
Use the tests for special causes to determine which observations you may need to investigate and to identify specific patterns and trends in your data. Each of the tests for special causes detects a specific pattern or trend in your data, which reveals a different aspect of process instability.
- One point more than 3 sigmas from center line
- Test 1 identifies subgroups that are unusual compared to other subgroups. Test 1 is universally recognized as necessary for detecting out-of-control situations. If small shifts in the process are of interest, you can use Test 2 to supplement Test 1 in order to create a control chart that has greater sensitivity.
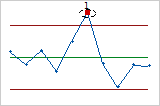
- Nine points in a row on same side of center line
- Test 2 identifies shifts in the process variation. If small shifts in the process are of interest, you can use Test 2 to supplement Test 1 in order to create a control chart that has greater sensitivity.
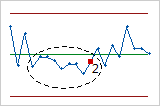
- Six points in a row, all increasing or all decreasing
- Test 3 detects trends. This test looks for long series of consecutive points that consistently increase in value or decrease in value.
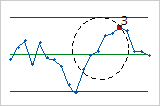
- Fourteen points in a row, alternating up and down
- Test 4 detects systematic variation. You want the pattern of variation in a process to be random, but a point that fails Test 4 might indicate that the pattern of variation is predictable.
Cumulative DPU Plot
The points on the Cumulative DPU plot show the mean DPU for each sample. The points are displayed in the order that the samples were collected. The middle horizontal line represents the mean DPU calculated from all the samples. The upper and lower horizontal lines represent the upper and lower confidence bounds for the mean DPU.
Interpretation
Use the Cumulative DPU plot to help you determine whether you have collected enough samples to have a stable estimate of the DPU.
Examine the defects per unit for the time-ordered samples to see how the estimate changes as you collect more samples. Ideally, the DPU should stabilize after several samples, as shown by a flattening of the plotted points along the mean DPU line.
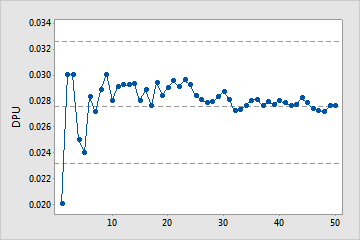
Enough samples
This capability study includes enough samples to estimate mean defects per unit.
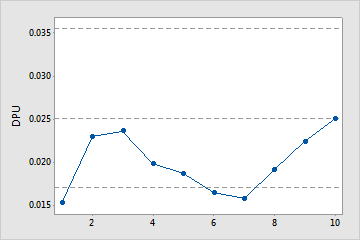
Not enough samples
This capability study does not include enough samples to estimate mean defects per unit.
Poisson Plot
The Poisson plot displays the observed number of defects versus the expected number of defects. The diagonal line shows where the data would fall if they perfectly followed the Poisson distribution. If the data stray significantly from this line, Poisson capability analysis may not provide reliable results.
Note
Minitab displays a Poisson plot when the subgroup sizes are equal. If the subgroup sizes vary, Minitab displays a defect rate plot. For more information, see the section on the Defect rate plot.
Interpretation
Use the Poisson plot to assess whether your data follow a Poisson distribution.
Examine the plot to determine whether the plotted points approximately follow a straight line. If not, then the assumption that the data were sampled from a Poisson distribution may be false.
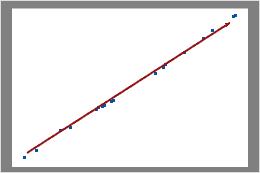
In these results, the data points fall closely along the line. You can assume that the data follow a Poisson distribution.
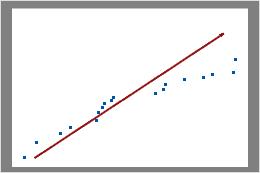
In these results, the data points do not fall along the line near the top right part of the plot. These data do not follow a Poisson distribution and cannot be reliably evaluated using Poisson capability analysis.
Defect Rate Plot
The defect rate plot displays the number of defects per unit (DPU) in each subgroup and the size of each subgroup. The center line equals the mean DPU.
Note
Minitab displays a defect rate plot when the subgroup sizes vary. If the subgroup sizes are constant, Minitab display a Poisson plot. For more information, see the section on the Poisson plot.
Interpretation
Use the defect rate plot to verify that your data is Poisson by checking the assumption that the number of defects per unit is constant across different sample sizes.
Examine the plot to assess whether the defects per unit (DPU) are randomly distributed across sample sizes or whether a pattern is present. If your data fall randomly about the center line, you conclude that the data follow a Poisson distribution.
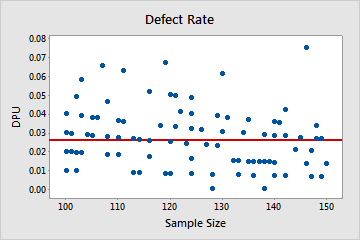
Poisson
In this plot, the points are scattered randomly around the center line. You can assume that the data follow a Poisson distribution.
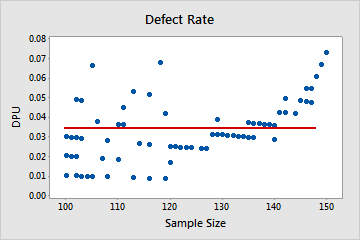
Not Poisson
In this plot, the pattern is not random. For sample size greater than 120, the DPU increases as the sample size increases. This result suggests a possible correlation between sample size and the rate of defects. Therefore, the data do not follow a Poisson distribution and cannot be reliably evaluated using Poisson capability analysis.
Histogram
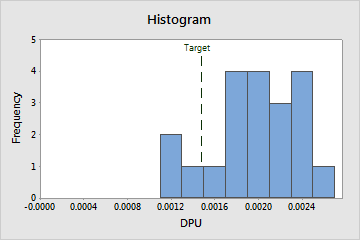
Interpretation
Use the distribution of DPU histogram to assess the distribution of the defects per unit of measurement in your samples.
Examine the peak and spread of the distribution of the defects per unit. The peak represents the most common values and approximates the center of the defects per unit. Assess the spread to understand how much the defects per unit varies across your samples.
Compare the reference line for the target value with the bars of the histogram. If your process is capable, most or all of the bars of the histogram should be to the left of the target value.
Mean DPU
The mean defects per unit (DPU) is the average defects per unit of measurement across the samples.
Interpretation
Use the mean DPU to estimate the average number of defects that you can expect for each unit and to determine whether your process meets customer expectations.
Compare the mean DPU with the target DPU to see whether the process meets requirements. If the mean DPU is higher than the target, you should improve your process.
You should also compare the target to the upper CI for DPU. If the upper CI is greater than the target, you cannot be confident that the mean DPU for your process is less than the target. You may need a larger sample size to determine with more confidence whether your process is on target.
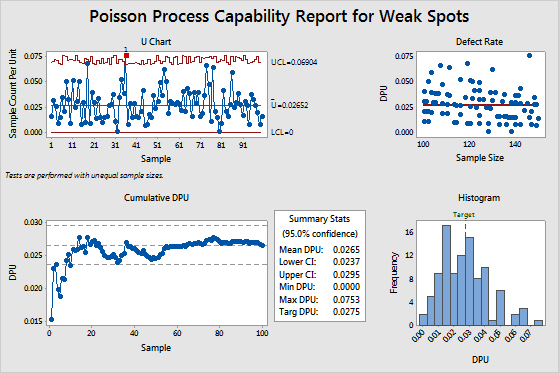
For example, in the Summary Stats table of the following output, the mean DPU (0.0265) is less than the target (0.0275). However, the upper CI is 0.0295, which is greater than the target. Although the process meets requirements, a larger sample size is needed to determine with more certainty whether the DPU is below the target.
Confidence interval (CI)
The confidence interval is a range of likely values for a capability index. The confidence interval is defined by a lower bound and an upper bound. The bounds are calculated by determining a margin of error for the sample estimate. The lower confidence bound defines a value that the capability index is likely to be greater than. The upper confidence bound defines a value that the capability index is likely to be less than.
Minitab displays both a lower confidence bound and an upper confidence bound for mean DPU.
Interpretation
Because samples of data are random, different samples collected from your process are unlikely to yield identical estimates of a capability index. To calculate the actual value of the capability index for your process, you would need to analyze data for all the items that the process produces, which is not feasible. Instead, you can use a confidence interval to determine a range of likely values for the capability index.
At a 95% confidence level, you can be 95% confident that the actual value of the capability index is contained within the confidence interval. That is, if you collect 100 random samples from your process, you can expect approximately 95 of the samples to produce intervals that contain the actual value of the capability index.
The confidence interval helps you to assess the practical significance of your sample estimate. When possible, compare the confidence bounds with a benchmark value that is based on process knowledge or industry standards.
For example, the maximum allowable mean defects per unit for a manufacturing process is 0.025%. Using Poisson capability analysis, analysts obtain a mean DPU estimate of 0.011%, which suggests that the process is capable. However, the upper CI for mean DPU is 0.029%. Therefore, the analysts cannot be 95% confident that the mean DPU of the population does not exceed the maximum allowable value. They may need to use a larger sample size or reduce the variability in the data to obtain a narrower confidence interval for the sample estimate.
Minimum DPU
Min DPU is the minimum defects per unit of measurement among the samples.
Interpretation
Use the minimum DPU to estimate the minimum number of defects that you can expect for each unit.
Maximum DPU
Max DPU is the maximum defects per unit of measurement among the samples.
Interpretation
Use the maximum DPU to estimate the maximum number of defects that you can expect for each unit.
Target DPU
The target DPU is the maximum number of defects per unit that you are willing to accept. If you did not specify a target DPU, Minitab assumes a target of 0 DPU.
Interpretation
Compare the mean DPU with the target DPU to see whether the process meets requirements. If the mean DPU is higher than the target, you should improve your process.
You should also compare the target to the upper CI for DPU. If the upper CI is greater than the target, you cannot be confident that the mean DPU for your process is less than the target. You may need a larger sample size to determine with more confidence whether your process is on target.

For example, in the Summary Stats table, the mean DPU (0.0265) is less than the target (0.0275). However, the upper CI for DPU is 0.0295, which is greater than the target. Although the process appears to meet requirements, you need a larger sample size to determine with more confidence whether the DPU is below the target.
