In This Topic
Xbar Chart
The Xbar chart plots the average of the measurements within each subgroup. The center line is the average of all subgroup averages. The control limits, which are set at a distance of 3 standard deviations above and below the center line, show the amount of variation that is expected in the subgroup averages.
Minitab displays an Xbar chart when your subgroup size is greater than 1.
Interpretation
Use an Xbar chart to monitor the mean of a process and determine whether it is stable enough to perform capability analysis.
Points located beyond the red control limits indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
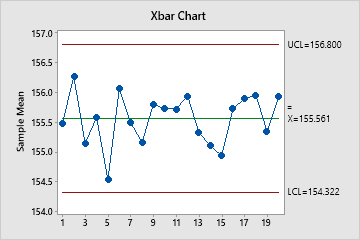
In these results, the points vary randomly around the center line and are within the control limits. No trends or patterns are present. The process center is stable enough to perform capability analysis.
I Chart
The I chart plots individual observations. The center line is an estimate of the process average. The control limits show the amount of variation that is expected in the individual sample values. For nonnormal data, Minitab estimates the probability density function from the data and uses this function to calculate the 0.135th and 99.865th percentiles. The values that correspond to these percentiles represent the lower and upper control limits.
Minitab displays an I chart when your subgroup size is 1.
Interpretation
Use an I chart to assess whether the individual measurements are in control and determine whether the process is stable enough to perform capability analysis.
Points located beyond the red control limits indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
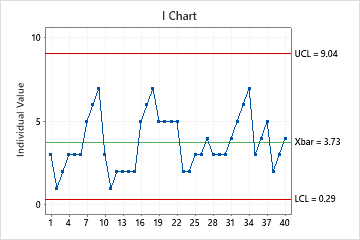
In this chart, the points vary randomly around the center line and are within the control limits. No trends or patterns are present. The process center is stable enough to perform capability analysis.
R Chart
The R chart plots the subgroup ranges. If the subgroup size is constant, then the center line is the average of all subgroup ranges. If the subgroup sizes differ, then the value of the center line depends on the subgroup size, because larger subgroups tend to have larger ranges. The control limits, which are set at a distance of 3 standard deviations above and below the center line, show the amount of variation that is expected in the subgroup ranges.
Minitab displays an R chart if your subgroup size is greater than 2 but less than 9.
Interpretation
Use an R chart to monitor the variation of a process and determine whether it is stable enough to perform capability analysis. The R chart indicates whether the subgroup-to-subgroup variation is in control.
Points located beyond the red control limits indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
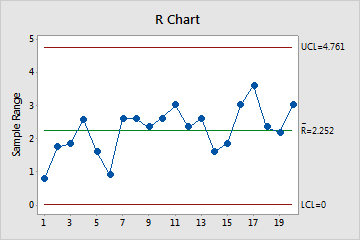
In these results, the points vary randomly around the center line and are within the control limits. No trends or patterns are present. The process variation is stable enough to perform capability analysis.
S Chart
The S chart plots the subgroup standard deviations. The center line represents the average of all subgroup standard deviations. The control limits, which are set at a distance of 3 standard deviations above and below the center line, are a visual display for the amount of variation that is expected in the subgroup standard deviations.
Minitab displays an S chart if your subgroup size is greater than or equal to 9.
Interpretation
Use an S chart to monitor the variation (standard deviation) of your process and determine whether it is stable enough to perform capability analysis. The S chart indicates whether the subgroup-to-subgroup variation is in control.
Points located beyond the red control limits indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
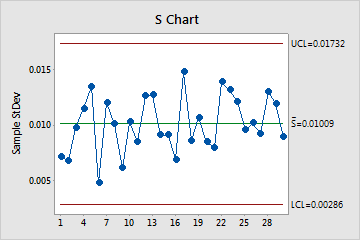
In these results, the points vary randomly around the center line and are within the control limits. No trends or patterns are present. The variation of the process is stable enough to perform capability analysis..
Moving range (MR) chart
The MR chart plots the moving ranges. The center line is the average of all moving ranges. The control limits, which are set at a distance of 3 standard deviations above and below the center line, show the amount of variation that is expected in the moving ranges.
Minitab displays an MR chart If your subgroup size is 1.
Interpretation
Use an MR chart to monitor the variation (moving range) of your process and to determine whether it is stable enough to perform capability analysis. The MR chart indicates whether the variation from observation to observation is in control.
Points located beyond the red control limits indicate that the process may not be stable and that the results of a capability analysis may not be reliable. You should identify the cause of out-of-control points and eliminate special-cause variation before you analyze process capability.
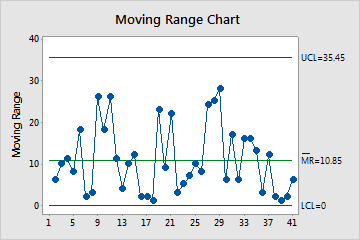
In these results, the points vary randomly around the center line and are within the control limits. No trends or patterns are present. The variation of the process is stable enough to perform capability analysis.
Last 25 Subgroups plot
The Last 25 Subgroups plot shows the data points for each of the last 25 subgroups and displays a line for the overall process mean.
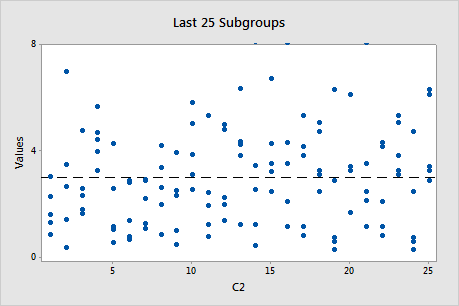
Interpretation
Use the Last 25 Subgroups plot to evaluate whether the distribution of the observations within the subgroups meets the requirements for your capability analysis.
- A subgroup that contains outliers
- Distribution changes across subgroups
If the plot shows evidence of problems or changes across subgroups, the capability results may not be valid. Investigate your process to determine why the data values are not distributed randomly across the subgroups.
Note
If your data has subgroup size of 1, Minitab displays a Last 25 Observations plot, which is interpreted similarly.
Capability Histogram
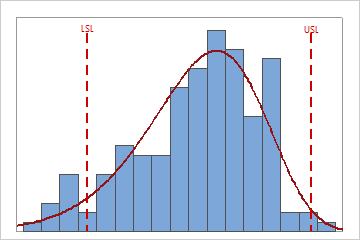
Interpretation
Use the capability histogram to visualize your sample data in relation to the distribution fit and the specification limits.
To visually assess the distribution fit, compare the bars in the histogram with the curved fit line. The shape of the data in the histogram should approximately match the curve. To ascertain whether the data follow the distribution, use the results in the probability plot.
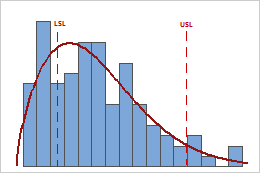
In these results, the process spread is larger than the specification spread, which suggests poor capability. Although much of the data are within the specification limits, there are many nonconforming items below the lower specification limit (LSL) and above the upper specification limit (USL).
Note
To determine the number of nonconforming items in your process use the overall PPM result.
Probability Plot
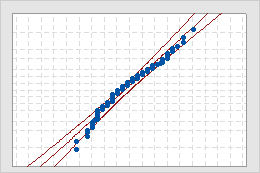
- Middle line
- The expected percentile from the distribution based on maximum likelihood parameter estimates.
- Confidence bound lines
- The left curved line indicates the lower bounds of the confidence intervals for the percentiles. The right curved line indicates the upper bounds of the confidence intervals for the percentiles.
- Anderson-Darling test statistic and p-value
- The results of a test to determine whether your data follow the distribution.
Interpretation
Use the probability plot to assess the fit of the nonnormal distribution used for the analysis.
If the distribution is a good fit for the data, the points should form an approximately straight line. Departures from this straight line indicate that the fit is unacceptable. If the p-value is greater than 0.05, you can assume that the data follow the nonnormal distribution used in the analysis.
If the p-value is less than 0.05, your data do not follow the selected distribution and the capability analysis results may not be accurate. Use Individual Distribution Identification to determine which nonnormal distribution or data transformation is more effective for your data.
Capability Plot
The capability plot is located at the lower right corner of the Nonnormal Capability Sixpack Report.
- The first interval represents the 6-σ interval from the standard normal distribution, which captures 99.74% of the process measurements.
- The specification interval represents the converted specification limits into the Z values using the selected nonnormal distribution and the standard normal distribution.
The process center is shown by the tick mark inside the Overall process spread interval.
Interpretation
Use the capability plot to visually assess the capability of your process.
To visually assess the overall capability of the process, compare the 6-σ interval with the specification interval on the plot. If the 6-σ interval is greater than the specification interval, then your process needs improvement. If the 6-sigma interval is contained within the specification interval, then you can conclude that the process is producing units that conform to specifications.
