Interpret the key results for Dotplot

Identify the peaks, which are the bins that have the most dots. The peaks represent the most common values in the sample. Assess the spread of your sample to understand how much your data varies.

For example, in this dotplot of customer wait times, the peak of the data occurs at about 6 minutes. The data spread is from about 3.5 minutes to 8.5 minutes.

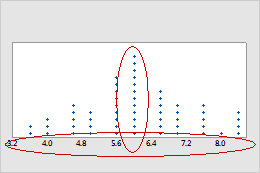
Investigate any surprising or undesirable characteristics on the dotplot. For example, the dotplot of customer wait times showed spread that is wider than expected. An investigation revealed that a software update to the computers caused instability and delays in customer wait times.

The sample size can affect the appearance of the graph.

For example, although these dotplots seem quite different, both of them were created using randomly selected samples of data from the same population. On the first dotplot, each symbol represents one observation. On the second dotplot, each symbol represents up to three observations.

n = 20

n = 100

A dotplot is best when the sample size is less than approximately 50. If the sample size is 50 or greater, a dot may represent more than one observation. Consider using a boxplot or a histogram in addition to the dotplot so that you can more easily identify primary characteristics of the distribution.

When data are skewed, the majority of the data are located on the high or low side of the graph. Skewness indicates that the data may not be normally distributed. Often, skewness is easiest to detect with a histogram or a boxplot.

These dotplots illustrate skewed data. The dotplot with right-skewed data shows wait times. Most of the wait times are relatively short, and only a few wait times are long. The dotplot with left-skewed data shows failure time data. A few items fail immediately and many more items fail later.

Right-skewed

Left-skewed

If you know that your data are not naturally skewed, investigate possible causes. If you want to analyze severely skewed data, read the data considerations topic for the analysis to make sure that you can use data that are not normal.

Outliers, which are data values that are far away from other data values, can strongly affect your results. Often, outliers are easiest to identify on a boxplot.

On a dotplot, unusually low or high data values identify possible outliers.

Try to identify the cause of any outliers. Correct any data entry or measurement errors. Consider removing data values that are associated with abnormal, one-time events (special causes). Then, repeat the analysis.

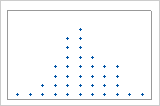
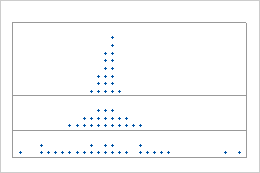
Multi-modal data have more than one peak. (A peak represents the mode of a set of data.) Multi-modal data usually occur when the data are collected from more than one process or condition, such as at more than one temperature.

For example, these dotplots are graphs of the same data. The simple dotplot has two peaks, but it is not clear what the peaks mean. The dotplot with groups shows that the peaks correspond to two groups.

Simple

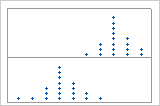
With groups

If you have additional information that allows you to classify the observations into groups, you can create a group variable with this information. Then, you can create the graph with groups to determine whether the group variable accounts for the peaks in the data.

Look for differences between the centers of the groups.

For example, these dotplots show the completion time for four versions of a credit card application. The center for each version of the credit card application is in a different location. The differences in the locations indicate that the completion times are different.

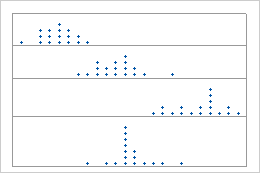
Paneled dotplots

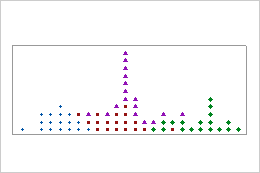
Stacked dotplots

Look for differences between the spreads of the groups.

For example, these dotplots show the weights of jars that were filled by three machines. Although the dotplots have almost the same center, some dotplots are wider and more spread out. The wider spread indicates that those machines fill jars less consistently.

Paneled dotplots

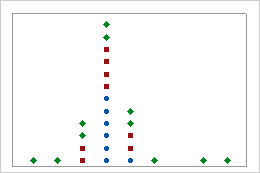
Stacked dotplots